MPI Fox Algorithm
Implementation of the Fox algorithm for square matrix multiplication using MPI

The objective of this project is to show the execution time and RAM usage of the algorithm for different matrix sizes and number of processes.
The program will run the algorithm for all the matrix sizes \( 2^x\ \forall\ x \in [n, m] \) five times and will calculate the average execution time and RAM usage. The results will be used to generate a graph that will be saved in the charts folder.
Developed by
José Felipe Marcial Rojas. Github
Miguel Ángel Hernández Moreno. Github
TO DO
- Add RAM measurement for Windows.
- Create CSV files with the results.
- Add a script to generate the charts from the CSV files.
- Add charts to docs page.
References
- Dean, N. (2017). Matrix Multiplication. https://www.cs.csi.cuny.edu/~gu/teaching/courses/csc76010/slides/Matrix%20Multiplication%20by%20Nur.pdf
- mpi4py. (2023). https://mpi4py.readthedocs.io/en/stable/
- Matplotlib (2023) https://matplotlib.org/
- Manim (2023) https://docs.manim.community/en/stable/
How It Works
This chapter is a detailed explanation of how the algorithm works, its implementation in Python and its dependencies, how to measure the time and ram memory consumption, as well as its graphing.
Algorithm Explanation
Checkerboard
Most parallel matrix multiplication functions use a checkerboard distribution of the matrices. This means that the processes are viewed as a grid, and, rather than assigning entire rows or entire columns to each process, we assign small sub-matrices. For example, if we have four processes, we might assign the element of a 4x4 matrix as shown below, checkerboard mapping of a 4x4 matrix to four processes.

Fox Algorithm
Fox‘s algorithm is a one that distributes the matrix using a checkerboard scheme like the above.
In order to simplify the discussion, lets assume that the matrices have order \(n\), and the number of processes, \(p\), equals \(n^2\). Then a checkerboard mapping assigns \(a_{ij}\), \(b_{ij}\) , and \(c_{ij}\) to process (\(i\), \(j\)).
Fox‘s algorithm takes \(n\) stages for matrices of order n one stage for each term aik bkj in the dot product
\(C_{i,j} = a_{i,0}b_{0,j} + a_{i,1}b_{1,i} +. . . +a_{i,n−1}b_{n−1,j}\)
Initial stage, each process multiplies the diagonal entry of A in its process row by its element of B:
Stage \(0\) on process\((i, j)\): \(c_{i,j} = a_{i,i} b_{i,j}\)
Next stage, each process multiplies the element immediately to the right of the diagonal of A by the element of B directly beneath its own element of B:
Stage \(1\) on process\((i, j)\): \(c_{i,j} = a_{i,i+1} b_{i+1,j}\)
In general, during the kth stage, each process multiplies the element k columns to the right of the diagonal of A by the element \(k\) rows below its own element of B:
Stage \(k\) on process\((i, j)\): \(c_{i,j} = a_{i,i+k} b_{i+k,j}\)
Example 2x2 Fox's Algorithm
Consider multiplying 2x2 block matrices \(A\), \(B\), \(C\):
\[ \begin{aligned} A \times B &= C \\ \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} &= \begin{bmatrix} 2 & 2 \\ 2 & 2 \end{bmatrix} \end{aligned} \]
Stage 0:
| Process (i, i mod 2) | Broadcast along row i |
|---|---|
| (0,0) | \(a_{00}\) |
| (1,1) | \(a_{11}\) |
\[ \begin{bmatrix} a_{00}, b_{00} & a_{00}, b_{01}\\ a_{11}, b_{10} & a_{11}, b_{11}\\ \end{bmatrix} \]
Process (\(i\), \(j\)) computes:
\[ \begin{aligned} C_{\text{Stage 0}} = \begin{bmatrix} 1 \times 1 & 1 \times 1 \\ 1 \times 1 & 1 \times 1 \end{bmatrix} &= \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \end{aligned} \]
Shift-rotate on the columns of \(B\)
Stage 1:
| Process (\(i\), (\(i\) + 1) mod 2) | Broadcast along row \(i\) |
|---|---|
| (0,1) | \(a_{01}\) |
| (1,0) | \(a_{10}\) |
\[ \begin{matrix} a_{01}, b_{10} & a_{01}, b_{11}\\ a_{10}, b_{00} & a_{10}, b_{01}\\ \end{matrix} \]
Process (\(i\), \(j\)) computes:
\[ \begin{aligned} C_{\text{Stage 1}} = \begin{bmatrix} 1+1 \times 1 & 1+1 \times 1 \\ 1+1 \times 1 & 1+1 \times 1 \end{bmatrix} &= \begin{bmatrix} 2 & 2 \\ 2 & 2 \end{bmatrix} \end{aligned} \]
Fox in Secuencial
- Imports
- Check Operating System and Define Constants
- Matrix Multiplication Function:**
- Matrix Initialization
- Matrix Multiplication Loop
- Print Results
- Main Execution
Sequential implementation of the Fox matrix multiplication algorithm. It initializes matrices, performs the multiplication, prints execution time and resource usage. The progress bar (tqdm) visualizes the iteration progress.
Imports
import os
import numpy as np
from sys import argv
from tqdm import tqdm
from time import perf_counter
We import necessary libraries, including os, numpy, sys, tqdm (for progress bar), and time.
Check Operating System and Define Constants
isLinux = os.name == 'posix'
if isLinux:
from resource import getrusage, RUSAGE_SELF
Determines if the operating system is Linux and imports resource-related functions for measuring resource usage.
Matrix Multiplication Function:**
def fox_SEC(exponent: int, isInt: bool) -> float:
Defines a function fox_SEC that takes the exponent and a flag isInt as parameters and returns the execution time.
Matrix Initialization
MATRIX_SIZE = 2**exponent
matrix_A = ...
matrix_B = ...
matrix_C = np.zeros((MATRIX_SIZE, MATRIX_SIZE), dtype=int) if isInt else np.zeros((MATRIX_SIZE, MATRIX_SIZE))
Initializes square matrices (A), (B), and (C) of size (2^{\text{exponent}} \times 2^{\text{exponent}}) with random integers or floats based on the isInt flag.
Matrix Multiplication Loop
start_time = perf_counter()
for x in tqdm(range(MATRIX_SIZE)):
for i in range(MATRIX_SIZE):
y = (x + i) % MATRIX_SIZE
matrix_C[i] += matrix_A[i, y] * matrix_B[y]
Performs matrix multiplication using nested loops. It calculates the product matrix (C) by iterating through rows and columns.
Print Results
print(perf_counter() - start_time)
print(getrusage(RUSAGE_SELF).ru_maxrss) if isLinux else print(0)
Prints the execution time and the RAM usage if the operating system is Linux.
Main Execution
if __name__ == '__main__':
fox_SEC(int(argv[1]), bool(argv[2]))
Calls the fox_SEC function with command-line arguments for exponent and isInt flag if we want matrices with integers or float type number.
Fox MPI
- Imports
- Check Operating System and Define Constants
- Command Line Arguments
- MPI Initialization
- Matrix Initialization on Rank 0
- Broadcast Data to All Processes
- Matrix Multiplication Loop
- MPI Allreduce
- Print Results
We use MPI to parallelize the matrix multiplication of randomly generated squared matrices A and B, and it calculates the product matrix C. The matrices are distributed among processes, and each process computes a portion of the final result. The MPI Allreduce function is used to combine the partial results from all processes.
Imports
import os
import numpy as np
from sys import argv
from mpi4py import MPI
from time import perf_counter
The code imports necessary libraries, including os, numpy, sys, mpi4py, and time. mpi4py is used for MPI (Message Passing Interface) communication in parallel computing.
Check Operating System and Define Constants
isLinux = os.name == 'posix'
Determines if the operating system is Linux.
if isLinux:
from resource import getrusage, RUSAGE_SELF
On Linux, it imports resource-related functions to measure resource usage.
Command Line Arguments
exponent = int(argv[1])
isInt = bool(argv[2])
Reads command line arguments: exponent and isInt. These are used to define the size of the matrices and the type of matrix elements.
MPI Initialization
comm = MPI.COMM_WORLD # get the communicator object
size = comm.Get_size() # total number of processes
rank = comm.Get_rank() # rank of this process
Initializes MPI communication, retrieves the total number of processes, and the rank of the current process.
Matrix Initialization on Rank 0
if rank == 0:
MATRIX_SIZE = 2**exponent
# generate two random matrices of size MATRIX_SIZE
# initialize the matrices A, B, and C
# matrices A and B contain random integers or floats based on 'isInt'
matrix_A = ...
matrix_B = ...
matrix_C = np.zeros((MATRIX_SIZE, MATRIX_SIZE), dtype=int) if isInt else np.zeros((MATRIX_SIZE, MATRIX_SIZE))
data = (MATRIX_SIZE, matrix_A, matrix_B, matrix_C)
else:
data = None
On the master process (rank 0), it initializes matrices A, B, and C, and packs the data into a tuple (data). Other processes receive None.
Broadcast Data to All Processes
data = comm.bcast(data, root=0) # broadcast the data to all processes
MATRIX_SIZE, matrix_A, matrix_B, matrix_C = data # unpack the data
All processes receive the data using MPI broadcast.
Matrix Multiplication Loop
start_time = perf_counter()
for x in range(MATRIX_SIZE):
if rank == x % size:
for i in range(MATRIX_SIZE):
y = (x + i) % MATRIX_SIZE
matrix_C[i] += matrix_A[i, y] * matrix_B[y]
Each process calculates a row of the matrix C. The rows are distributed among processes, and the multiplication is performed locally.
MPI Allreduce
comm.Allreduce(MPI.IN_PLACE, matrix_C, op=MPI.SUM)
MPI Allreduce function is used to sum the rows of matrix C calculated by each process.
Print Results
if rank == 0:
print(perf_counter() - start_time)
print(getrusage(RUSAGE_SELF).ru_maxrss) if isLinux else print(0)
The master process prints the execution time and the RAM memory usage if the operating system is Linux.
Time and Memory Measurement
This code measures the execution time and memory consumption using the time and resource modules. Let's break down how the time and memory measurements are implemented:
Time Measurement
The perf_counter function from the time module is used to measure the execution time.
start_time = perf_counter()
# ... (code to be measured)
print(perf_counter() - start_time)
start_timeis recorded usingperf_counter()before the code to be measured.- The execution time is calculated by subtracting
start_timefrom the current time after the code has executed. - The result is printed, representing the time taken for the code to run.
Memory Consumption Measurement (RAM)
getrusageonly works in linux/unix and FreeBSD operative systems based, therefore, this functionality is disabled in windows. For more compatibility information check the resource library docs.
The getrusage function from the resource module is used to measure the maximum resident set size, which is an indicator of memory consumption.
print(getrusage(RUSAGE_SELF).ru_maxrss) if isLinux else print(0)
getrusage(RUSAGE_SELF).ru_maxrssretrieves the maximum consumption of RAM used by the process.- This value is printed only if the operating system is Linux (
isLinuxisTrue); otherwise, it prints 0.
Charts Generator
We have used the matplotlib and manim library to represent the comparison of the execution times and memory usage of the Fox algorithm with matrices of either integers or floats.
Matplotlib
Calculate Mean Times and Memory Usage
times_MPI, times_SEC, memory_MPI, memory_SEC = data(min_e, max_e, isInt=isInt)
Calls the data function to obtain execution times and memory usage for sequential and parallel executions.
Prepare Data for Plotting
y_Time_MPI = [np.mean(times_MPI [exponent]) for exponent in times_MPI ]
y_Time_SEC = [np.mean(times_SEC [exponent]) for exponent in times_SEC ]
y_Memory_MPI = [np.mean(memory_MPI[exponent]) for exponent in memory_MPI]
y_Memory_SEC = [np.mean(memory_SEC[exponent]) for exponent in memory_SEC]
Calculates the mean times and memory usage for both MPI and sequential executions.
Configure Bar Chart Parameters
bar_w = 0.35
x_Time_MPI = np.array([exponent - bar_w/2 for exponent in times_MPI])
x_Time_SEC = np.array([exponent + bar_w/2 for exponent in times_SEC])
x_Memory_MPI = np.array([exponent - bar_w/2 for exponent in memory_MPI])
x_Memory_SEC = np.array([exponent + bar_w/2 for exponent in memory_SEC])
Sets parameters for the bar chart, including bar width and positions for both time and memory plots.
Create Matplotlib Figure
fig, (Time_ax, Memory_ax) = plt.subplots(1, 2, figsize=(20, 5)) if isLinux else plt.subplots(1, 1, figsize=(10, 5))
Creates a Matplotlib figure with one or two subplots, depending on whether the operating system is Linux.
Configure Plot Titles and Labels
fig.suptitle(f'Comparison of Fox Algorithm Executions with {num_type} numbers.\n{PROCESSOR} - {nthreads} Threads - {RAM}GB')
Time_ax.set_title('Sequential and Parallel Execution Time Comparison')
Time_ax.set_xlabel('Matrix Order')
Time_ax.set_ylabel('Execution Time (s)')
Sets titles and labels for the plots.
Plot Execution Time Bars
bars_Time_MPI = Time_ax.bar(x_Time_MPI, y_Time_MPI, bar_w, label='MPI', color='#EA75FA')
bars_Time_SEC = Time_ax.bar(x_Time_SEC, y_Time_SEC, bar_w, label='Sequential', color='#4590FA')
Plots bars for execution times for both MPI and sequential executions.
Plot Memory Usage Bars
In the background we use
getrusage. This function only works in linux/unix and FreeBSD operative systems based, therefore, this functionality is disabled in windows. For more compatibility information check the resource library docs.
if isLinux:
Memory_ax.set_title('Memory Usage (RAM) Comparison')
Memory_ax.set_xlabel('Matrix Order')
Memory_ax.set_ylabel('Memory Used (MB)')
bars_Memory_MPI = Memory_ax.bar(x_Memory_MPI, y_Memory_MPI, bar_w, label='MPI', color='#EA75FA')
bars_Memory_SEC = Memory_ax.bar(x_Memory_SEC, y_Memory_SEC, bar_w, label='Sequential', color='#4590FA')
Plots bars for memory usage for both MPI and sequential executions.
Display Labels and Legends
for bar in bars_Time_SEC + bars_Time_MPI:
x_pos = bar.get_x() + bar.get_width()/2.0
y_value = bar.get_height()
Time_ax.text(x_pos, y_value, f'{y_value:5.5}s', va='bottom', ha='center')
Time_ax.legend()
if isLinux:
for bar in bars_Memory_SEC + bars_Memory_MPI:
x_pos = bar.get_x() + bar.get_width()/2.0
y_value = bar.get_height()
Memory_ax.text(x_pos, y_value, f'{(y_value/1024):5.5}MB', va='bottom', ha='center')
Memory_ax.legend()
Displays labels and legends on the plots.
Save Plots
plt.tight_layout()
fig.savefig(create_dir('charts', f'{2**(min_e)}-{2**(max_e-1)}', 'int' if isInt else 'float'))
Saves the plots to a file.
Manim
This Manim script defines a scene that creates an animated bar chart using data from different matrix multiplication scenarios. The script loops over various parameters, generates animations, and saves the results in an organized directory structure.
Manim Scene Class
class chart(Scene):
def construct(self):
Defines a Manim scene class named chart.
Configure Frame Dimensions
config["frame_width"] = 12
config["frame_height"] = 8
Sets the width and height of the animation frame.
Create Bar Chart
chart = BarChart(
values = np.zeros(len(data)),
y_range=[0, round(max_v + max_v/8,2), round(max_v/4,2)],
x_length=16,
y_length=6,
bar_width=0.8,
bar_names=[2**exp for exp in EXP],
y_axis_config={"font_size": 24},
x_axis_config={"font_size": 24},
).scale(0.7)
Creates a bar chart using Manim's BarChart class with specified configurations.
Create Axes Labels
x_label = chart.get_x_axis_label('Matrix Size', edge=DOWN, direction=DOWN, buff=0.05).scale(0.6)
y_l = 'Time (s)' if MEASURE == 'time_mean' else 'Memory (MB)'
y_label = chart.get_y_axis_label(y_l, edge=UP, direction=UP, buff=-1).scale(0.6).rotate(PI/2).next_to(chart, LEFT)
Adds labels for the x-axis and y-axis.
Create Group for Chart and Labels
gv = VGroup(chart, x_label, y_label).to_edge(DOWN)
Groups the chart and labels together.
Create Title and Architecture Information
Title = f'Comparison of RAM used by the Fox algorithm with {dt} numbers using the {meth} method' if MEASURE == 'memory_mean' else f'Comparison of execution time of the Fox algorithm with {dt} numbers using the {meth} method'
t_top = Tex(Title).scale(0.75).to_edge(UP)
architecture = Tex(f'{PROCESSOR} {THREADS} {RAM} DDR4 3200MHz', color='purple_a').scale(0.6).next_to(t_top, DOWN)
Creates a title and information about the system architecture.
Display Elements
self.play(Create(gv), Create(t_top), Create(architecture))
Displays the grouped chart, labels, title, and architecture information.
Animate Chart Bars
self.play(chart.animate.change_bar_values(data), run_time=1.5)
Animates the bars in the chart based on the data.
Display Bar Labels
self.play(Create(chart.get_bar_labels(font_size=30, color=WHITE)))
Displays labels for the bars in the chart.
Save and Display Animation
self.wait(3)
Waits for 3 seconds before completing the animation.
Main Execution Loop
if __name__ == '__main__':
# Loop over different parameters (DTYPE, METHOD, EXP) and generate animations for each case.
Uses nested loops to iterate over different data parameters and create animations for each case.
Move Generated Files
shutil.move('manim/media/images/chart.png', f'{path}/{file}.png')
shutil.move('manim/media/videos/720p30/chart.mp4', f'{path}/{file}.mp4')
Moves the generated image and video files to a specified directory.
Results
AMD Ryzen 5 3600
Characteristics
- 6 Core Processor 12 Threads
- 16GB RAM DDR3
- Windows 11
Float
Float Sequential Time
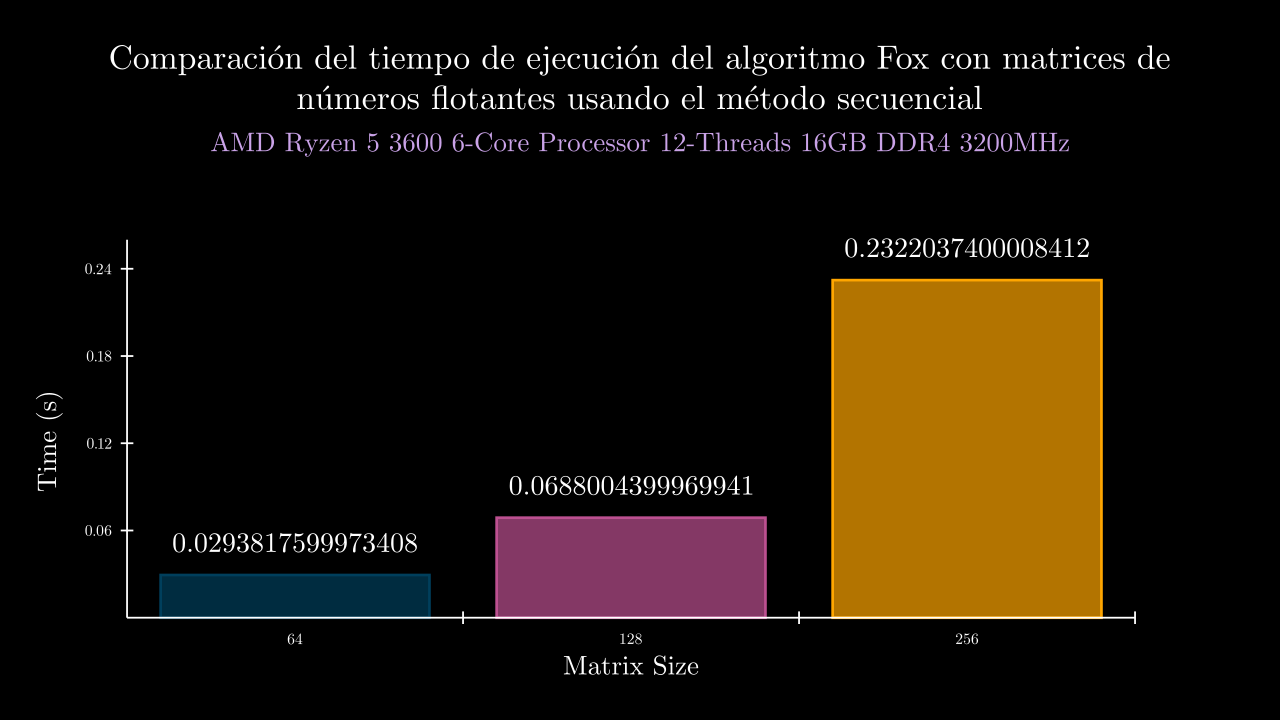
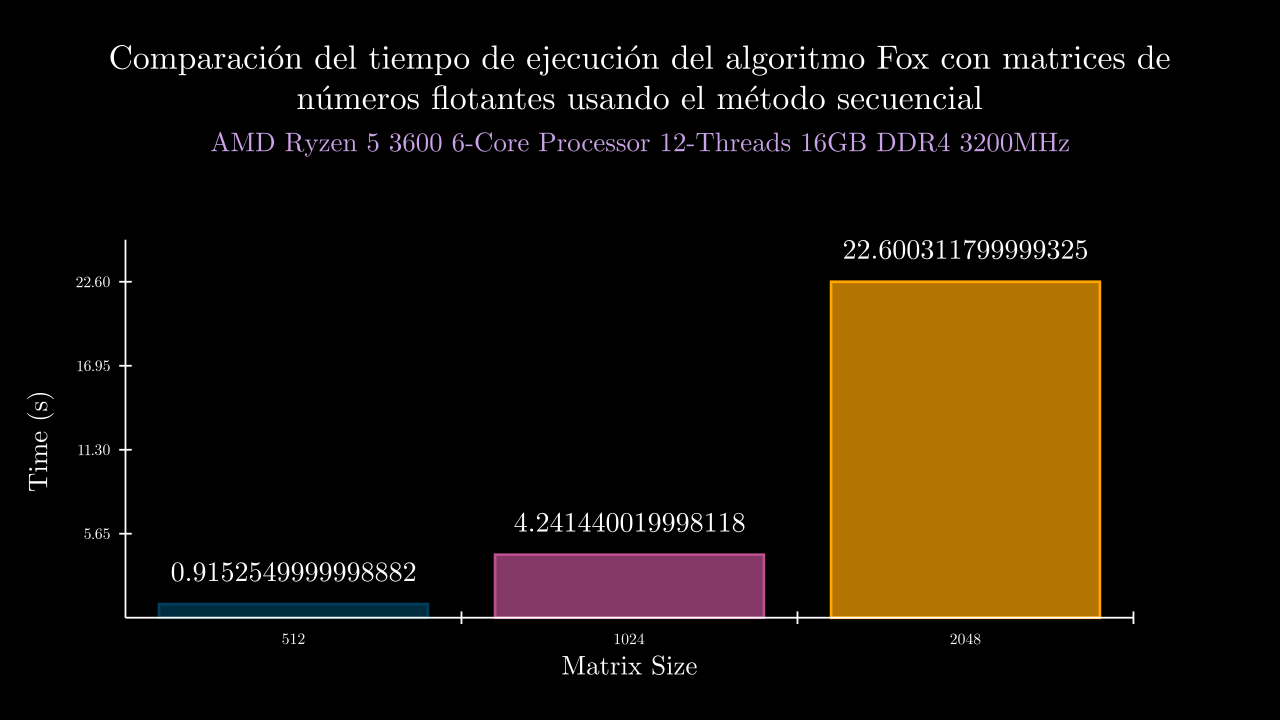
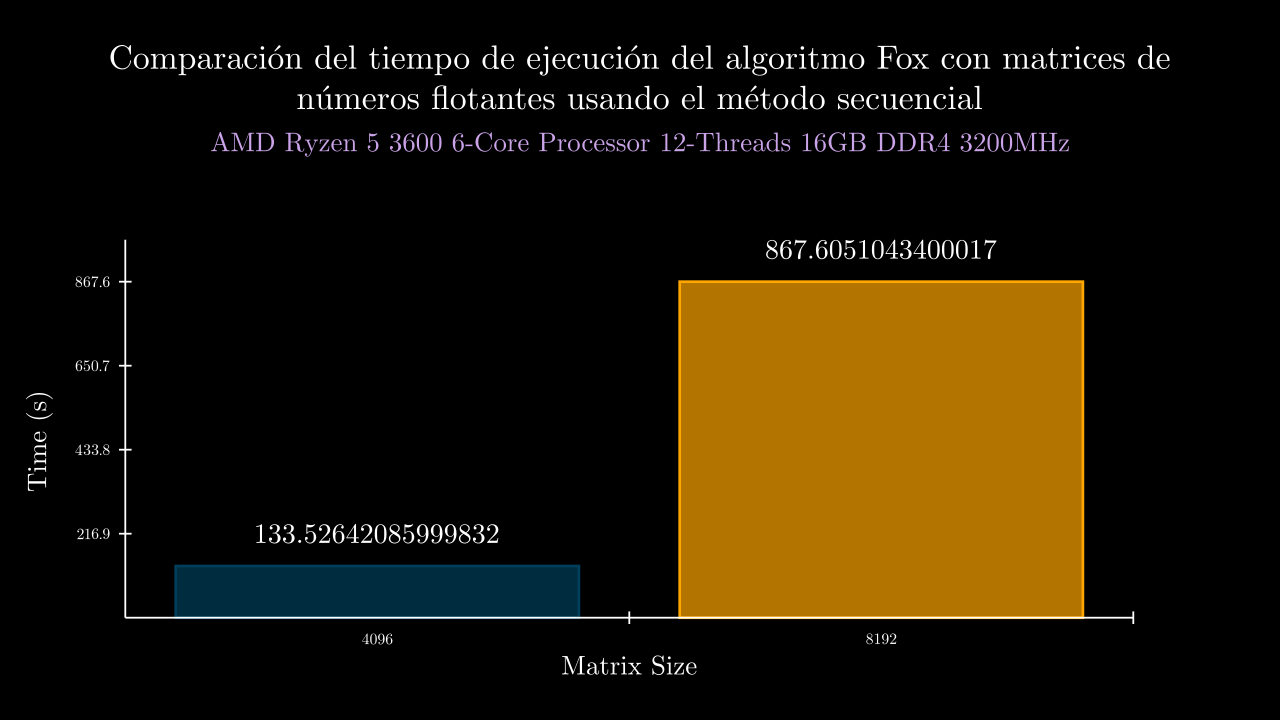
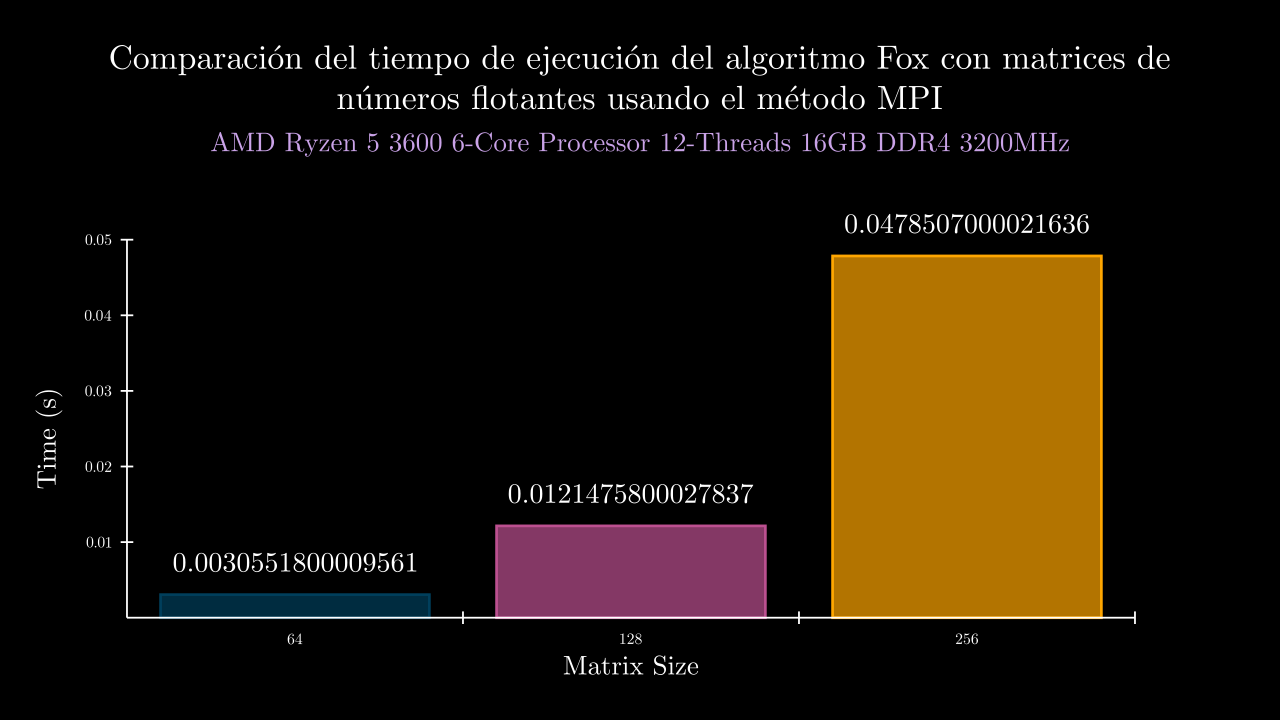
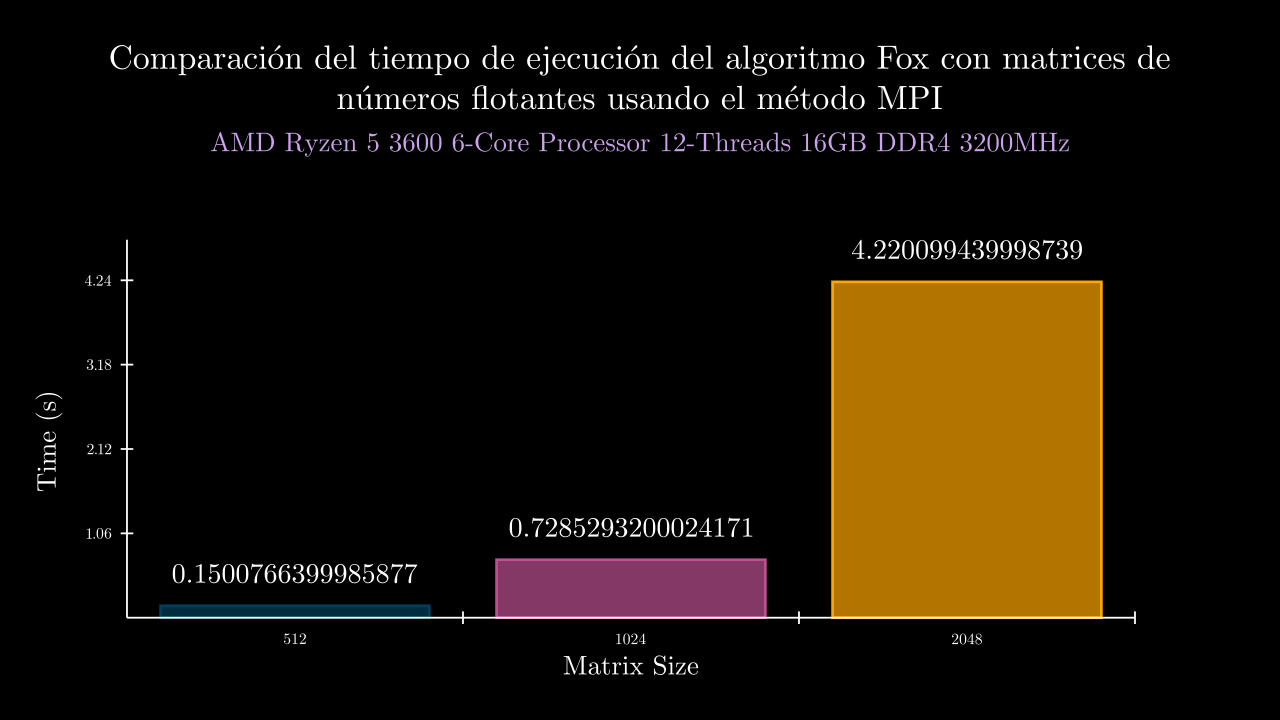
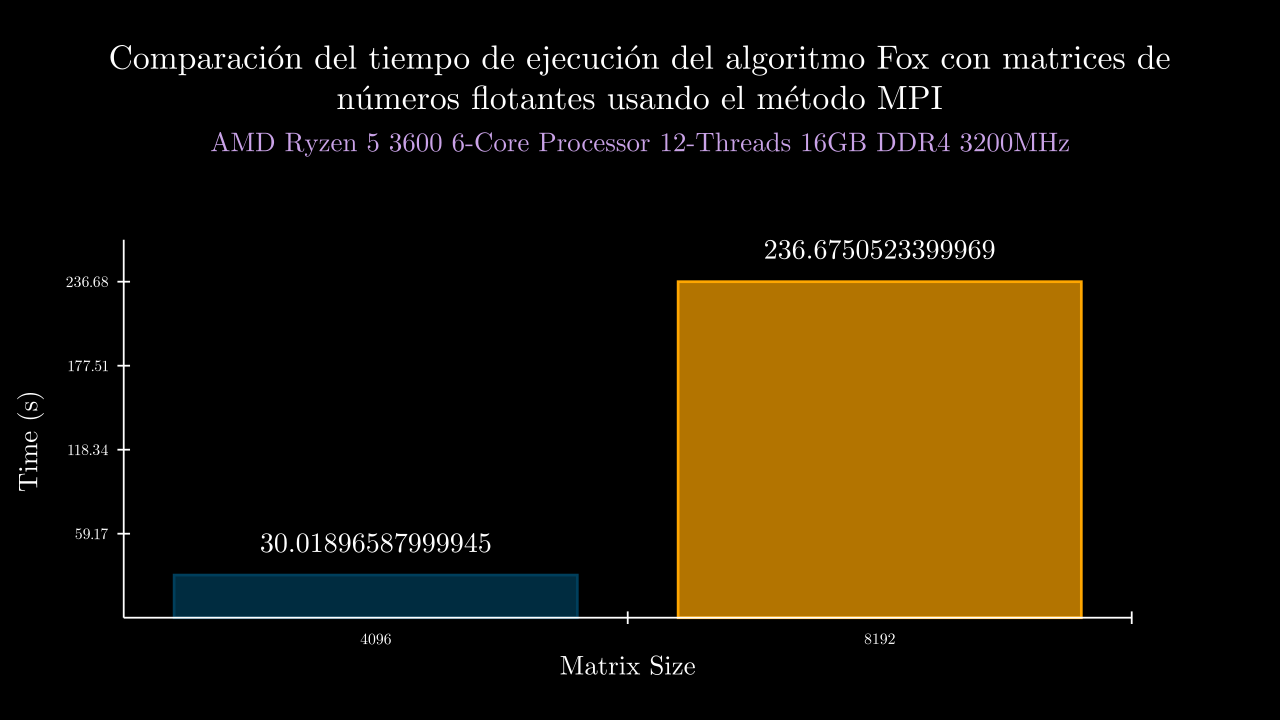
Float MPI Time
| exponent | time_mean | memory_mean | t1 | t2 | t3 | t4 | t5 | m1 | m2 | m3 | m4 | m5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 MPI | 0.0030551800009561703 | 0.0 | 0.003443099994910881 | 0.003591700005927123 | 0.002645799992023967 | 0.0024062000011326745 | 0.0031891000107862055 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 7 MPI | 0.012147580002783797 | 0.0 | 0.008701600003405474 | 0.007411400001728907 | 0.011636200011707842 | 0.012634700004127808 | 0.020353999992948957 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 8 MPI | 0.04785070000216365 | 0.0 | 0.06328279999434017 | 0.06804290000582114 | 0.04427630000282079 | 0.031611700003850274 | 0.032039800003985874 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 9 MPI | 0.15007663999858778 | 0.0 | 0.14042419999896083 | 0.14926969999214634 | 0.17817379999905825 | 0.13948559999698773 | 0.14302990000578575 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 10 MPI | 0.7285293200024171 | 0.0 | 0.7056575000024168 | 0.7311181999975815 | 0.7229602000006707 | 0.741693200005102 | 0.7412175000063144 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 11 MPI | 4.220099439998739 | 0.0 | 4.461288599995896 | 4.156596500004525 | 4.157651299989084 | 4.154624900009367 | 4.170335899994825 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 12 MPI | 30.01896587999945 | 0.0 | 29.88082619999477 | 30.08790269999008 | 30.047352100009448 | 30.123827899995376 | 29.954920500007574 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 13 MPI | 236.6750523399969 | 0.0 | 237.7994949999993 | 235.69214719999582 | 236.10693409999658 | 236.1462773999956 | 237.63040799999726 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 6 SEC | 0.02938175999734085 | 0.0 | 0.029565399992861785 | 0.028534299999591894 | 0.028825000001234002 | 0.030017799988854676 | 0.029966300004161894 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 7 SEC | 0.0688004399969941 | 0.0 | 0.06092390000412706 | 0.061088000002200715 | 0.07383909999043681 | 0.06472219999704976 | 0.08342899999115616 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 8 SEC | 0.2322037400008412 | 0.0 | 0.2795788000075845 | 0.22014479999779724 | 0.2378789000067627 | 0.21173860000271816 | 0.21167759998934343 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 9 SEC | 0.9152549999998882 | 0.0 | 0.919658899991191 | 0.9154974999983096 | 0.9178280000051018 | 0.9052672000107123 | 0.9180233999941265 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 10 SEC | 4.241440019998118 | 0.0 | 4.196437299993704 | 4.21114800000214 | 4.252561899993452 | 4.347026300005382 | 4.200026599995908 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 11 SEC | 22.600311799999325 | 0.0 | 22.48826499999268 | 22.77492300000449 | 22.643439200008288 | 22.542179099997156 | 22.552752699994016 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 12 SEC | 133.52642085999832 | 0.0 | 133.1521122999984 | 133.94261509999342 | 133.40880069999548 | 133.72657189999882 | 133.4020043000055 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 13 SEC | 867.6051043400017 | 0.0 | 861.1038434999937 | 863.3430384000094 | 882.7370500000106 | 865.974721999999 | 864.8668677999958 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
Integer
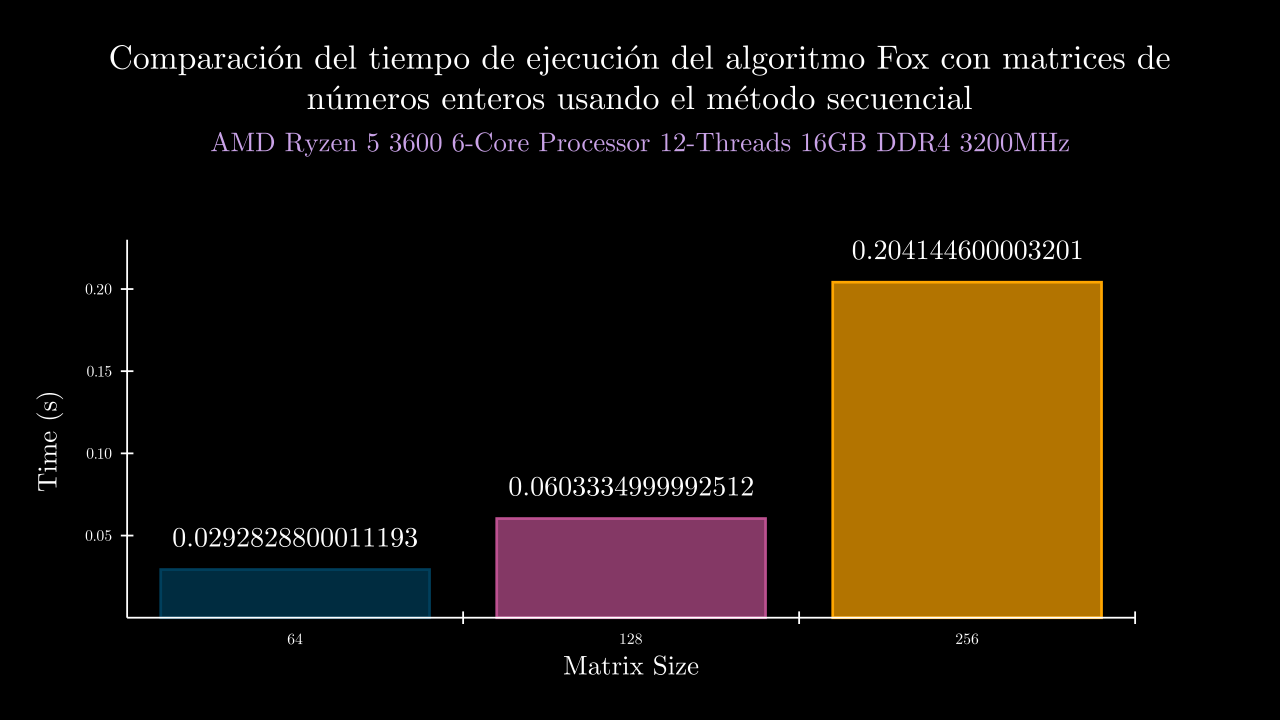
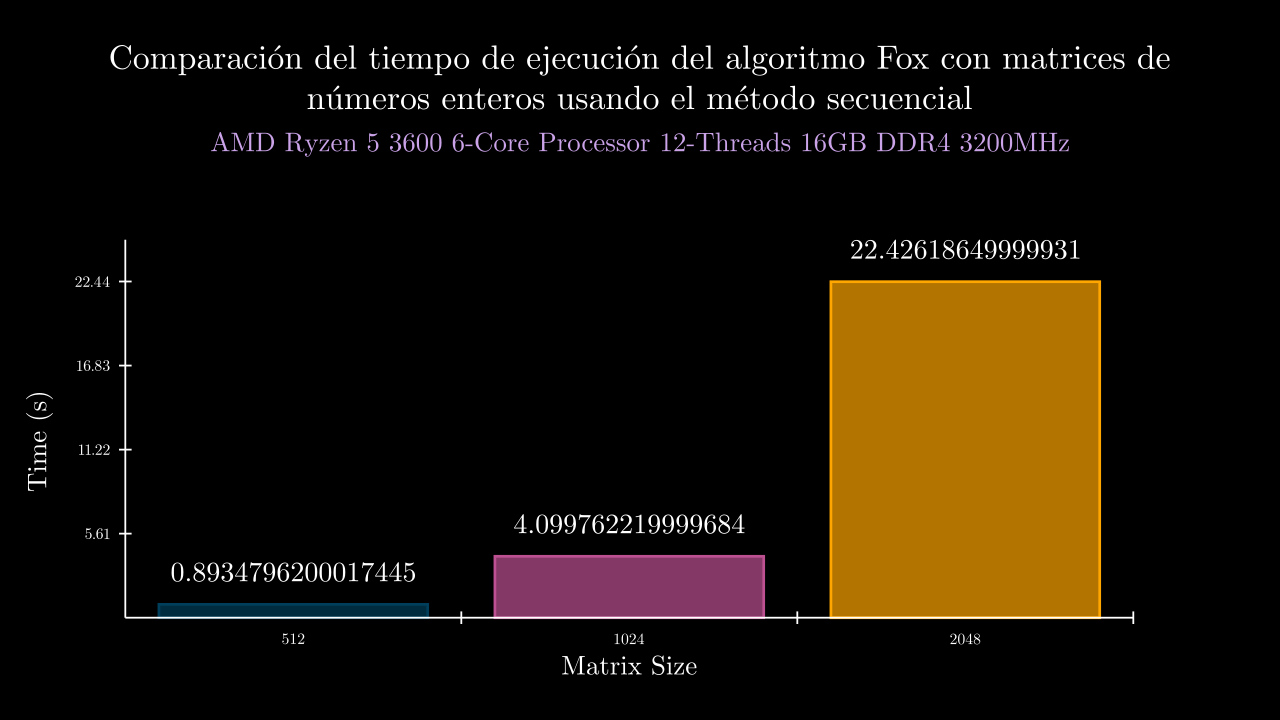
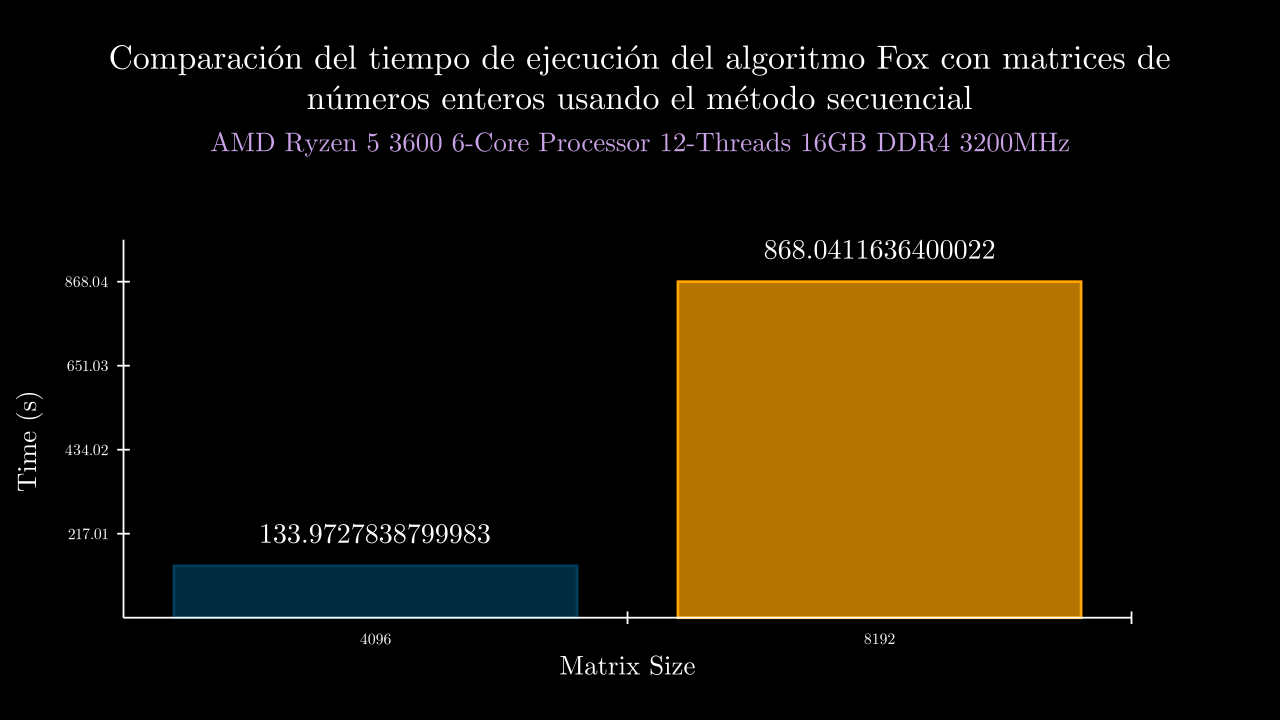
Integer Sequential Time
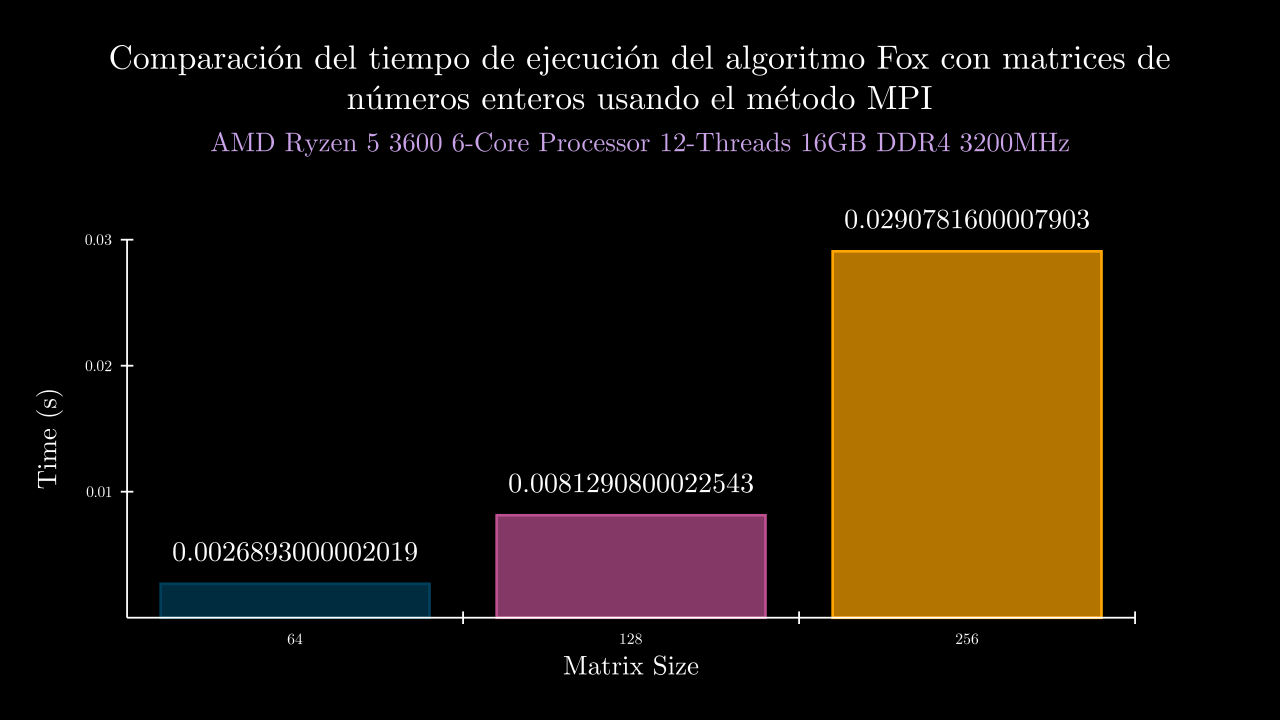
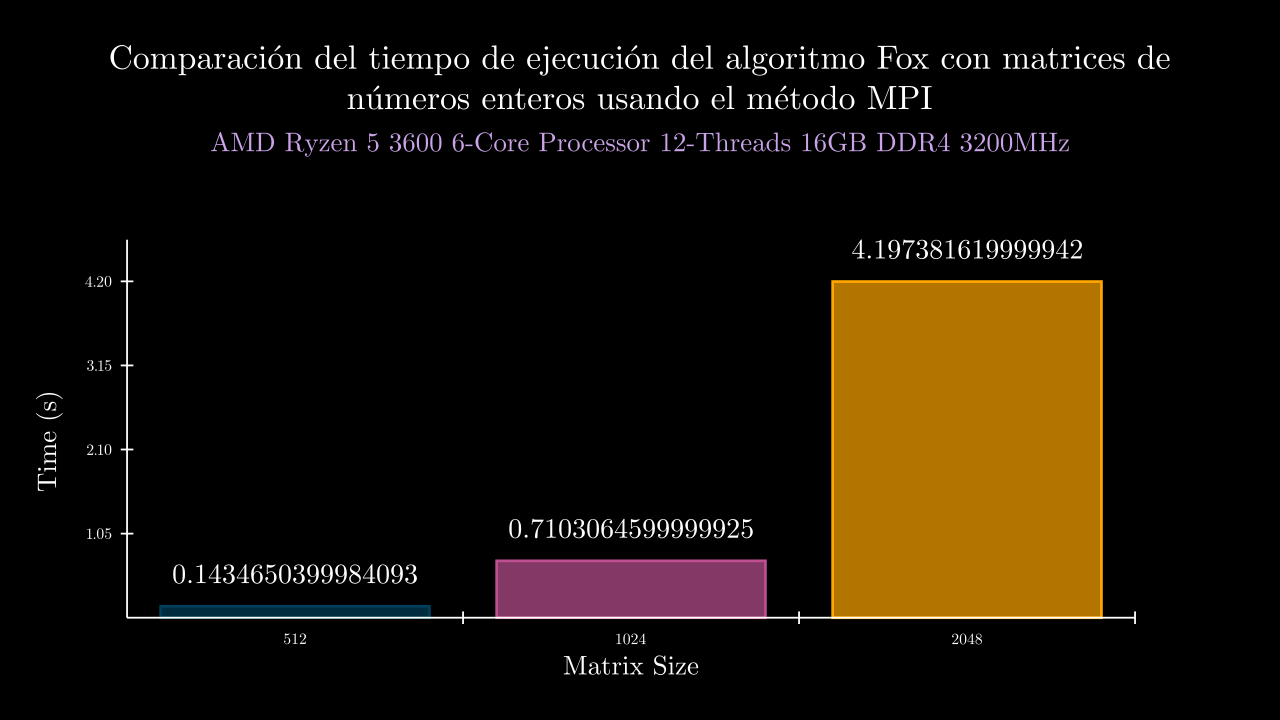
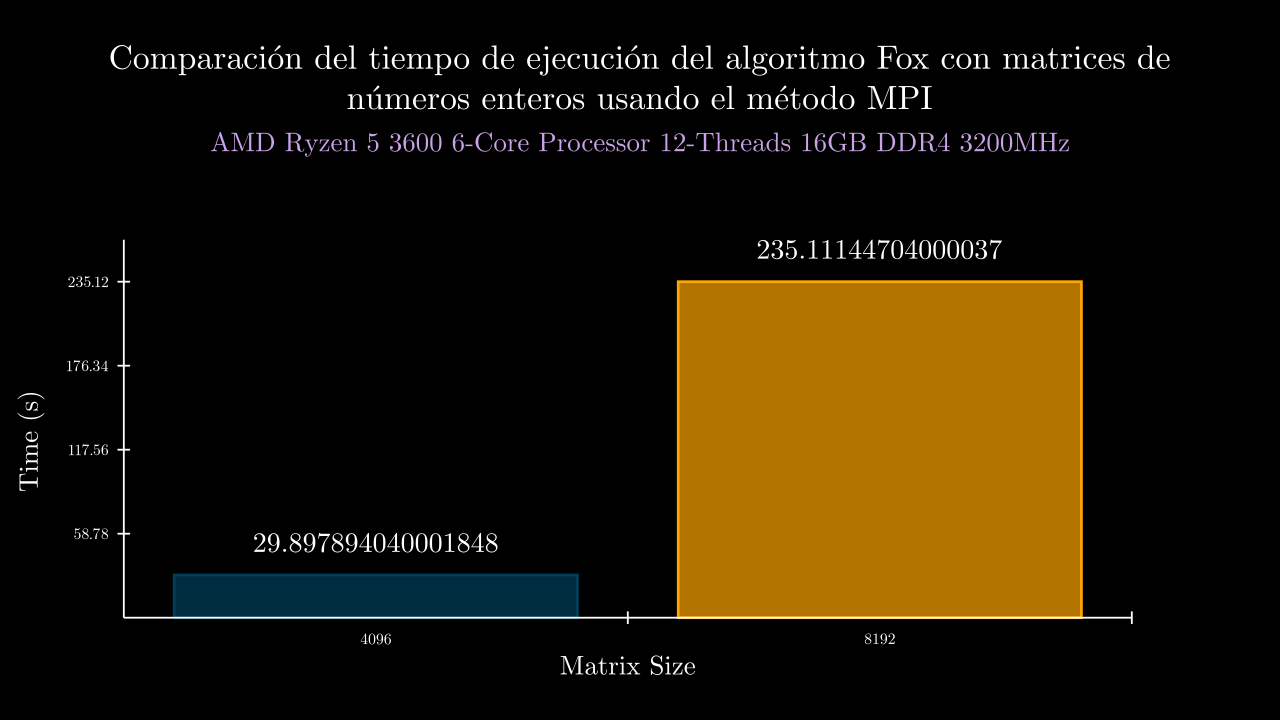
Integer MPI Time
| exponent | time_mean | memory_mean | t1 | t2 | t3 | t4 | t5 | m1 | m2 | m3 | m4 | m5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 MPI | 0.002689300000201911 | 0.0 | 0.0023728000014671125 | 0.0031310999984270893 | 0.003193299999111332 | 0.002304499997990206 | 0.002444800004013814 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 7 MPI | 0.008129080002254341 | 0.0 | 0.007357000002230052 | 0.007035200003883801 | 0.010785200000100303 | 0.007353400003921706 | 0.008114600001135841 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 8 MPI | 0.029078160000790377 | 0.0 | 0.03505410000070697 | 0.02448770000046352 | 0.02802230000088457 | 0.028654599998844787 | 0.029172100003052037 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 9 MPI | 0.14346503999840934 | 0.0 | 0.13513329999841517 | 0.1567471999951522 | 0.1323597000009613 | 0.14503549999790266 | 0.14804949999961536 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 10 MPI | 0.7103064599999925 | 0.0 | 0.7079091999985394 | 0.7368706999986898 | 0.7045027999993181 | 0.7158186000015121 | 0.6864310000019032 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 11 MPI | 4.197381619999942 | 0.0 | 4.1438114999982645 | 4.2107729999988806 | 4.155224800000724 | 4.293355500005418 | 4.183743299996422 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 12 MPI | 29.897894040001848 | 0.0 | 30.06699220000155 | 30.016745799999626 | 29.889804500002356 | 29.83930820000387 | 29.676619500001834 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 13 MPI | 235.11144704000034 | 0.0 | 236.3504993000024 | 234.47165250000398 | 233.7182845999996 | 233.5796835000001 | 237.43711529999564 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 6 SEC | 0.029282880001119338 | 0.0 | 0.030714400003489573 | 0.029131399998732377 | 0.029304000003321562 | 0.028636000002734363 | 0.028628599997318815 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 7 SEC | 0.060333499999251215 | 0.0 | 0.06073800000012852 | 0.05998159999580821 | 0.06019219999870984 | 0.060492800002975855 | 0.06026289999863366 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 8 SEC | 0.20414460000320106 | 0.0 | 0.20137200000317534 | 0.2014608000026783 | 0.20306750000600005 | 0.2043989000012516 | 0.21042380000289995 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 9 SEC | 0.8934796200017445 | 0.0 | 0.8970133000038913 | 0.8909725000048638 | 0.8946256999988691 | 0.8927302000010968 | 0.8920564000000013 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 10 SEC | 4.099762219999684 | 0.0 | 4.0990553999945405 | 4.08489499999996 | 4.108394100003352 | 4.1030172999962815 | 4.103449300004286 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 11 SEC | 22.42618649999931 | 0.0 | 22.355210499998066 | 22.41438790000393 | 22.40389960000175 | 22.536025899993547 | 22.421408599999268 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 12 SEC | 133.9727838799983 | 0.0 | 134.05730229999608 | 133.69151380000403 | 134.34823799999867 | 134.0702519999977 | 133.69661329999508 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 13 SEC | 868.0411636400022 | 0.0 | 864.2142595000041 | 865.9321351000035 | 870.7643005000064 | 871.6217934000015 | 867.6733296999955 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
AMD Ryzen 3 5300U with Radeon Graphics
Characteristics
- 4 Threads
- 8 GB RAM
- Ubuntu 20.01 LTS
Float
Float Sequential Time
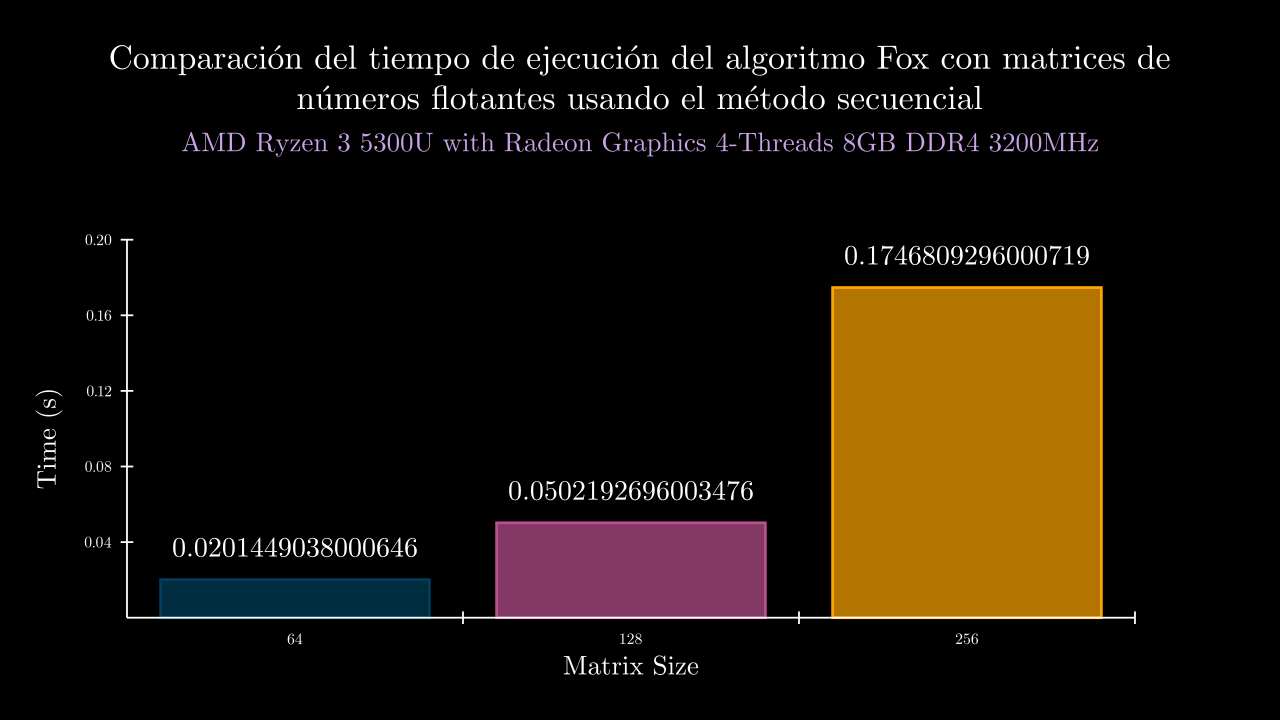
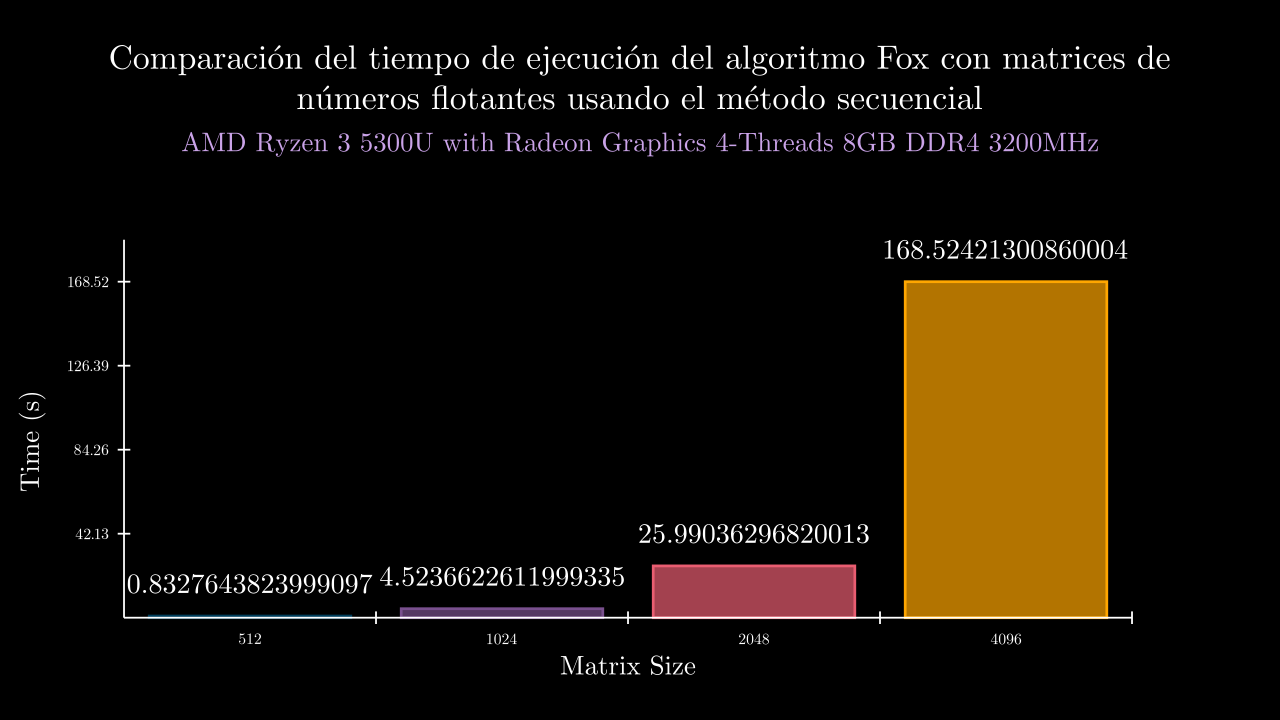
Float Sequential Memory
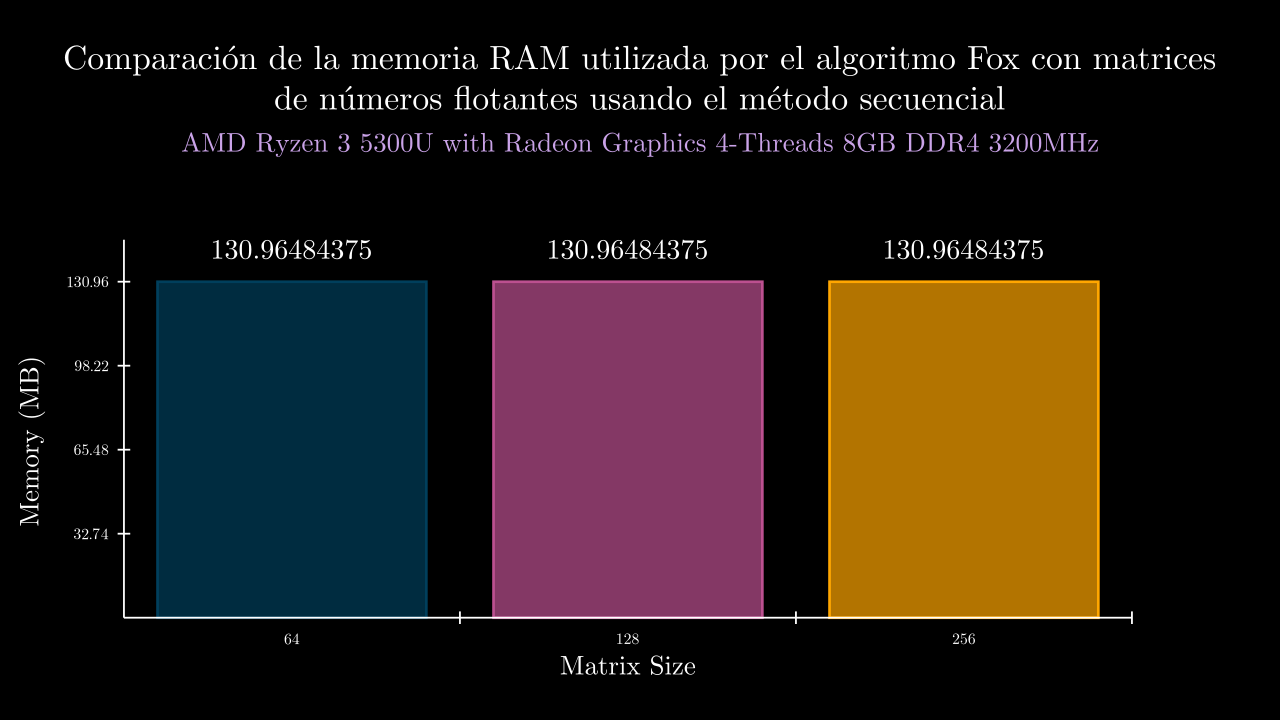
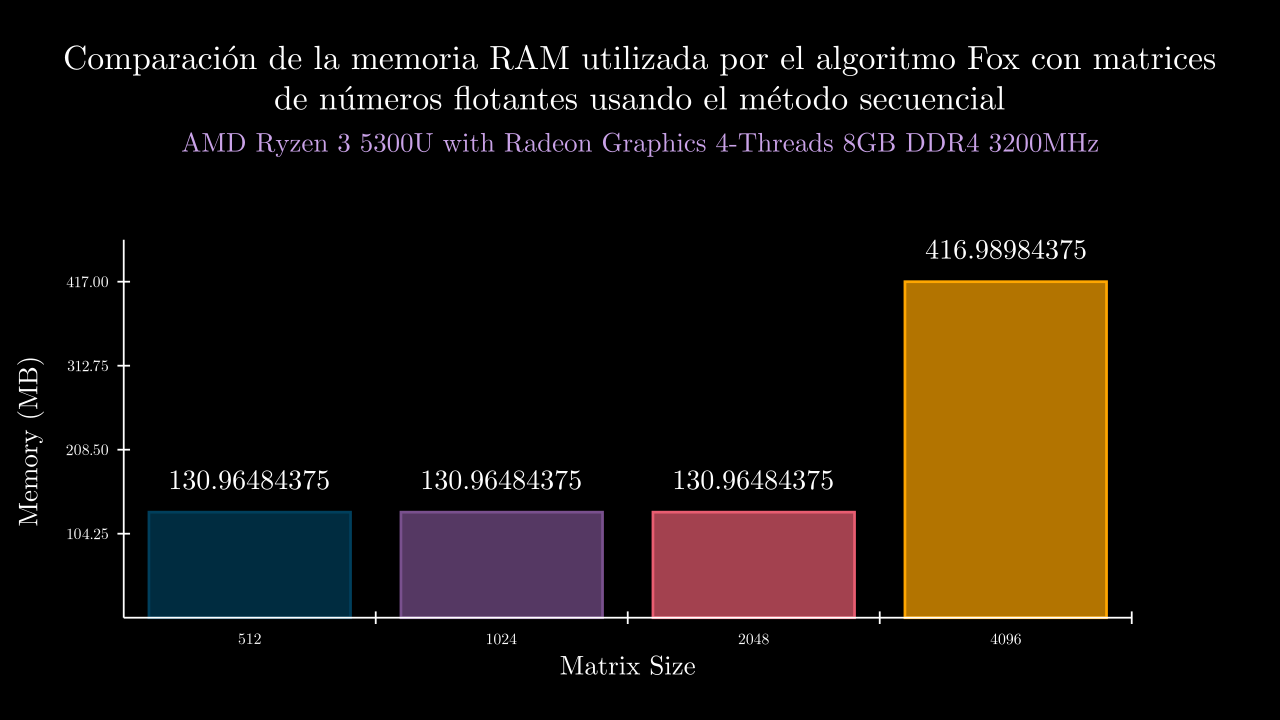
Float MPI Time
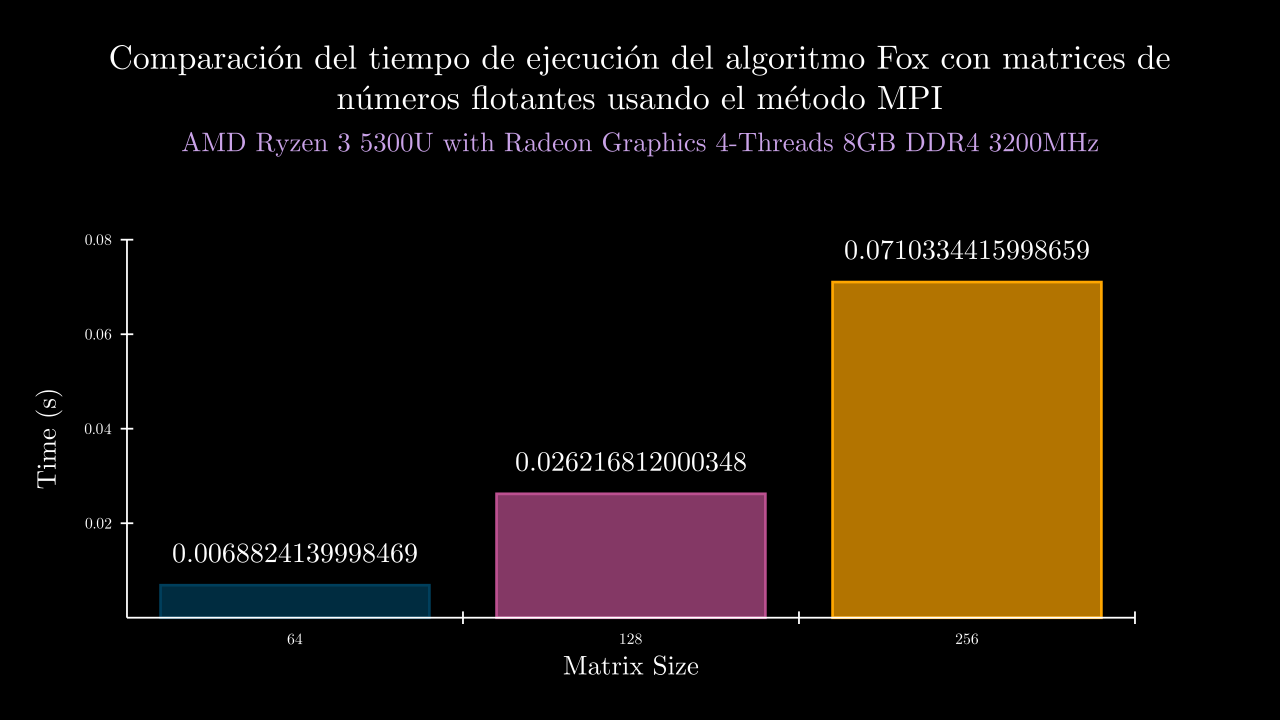
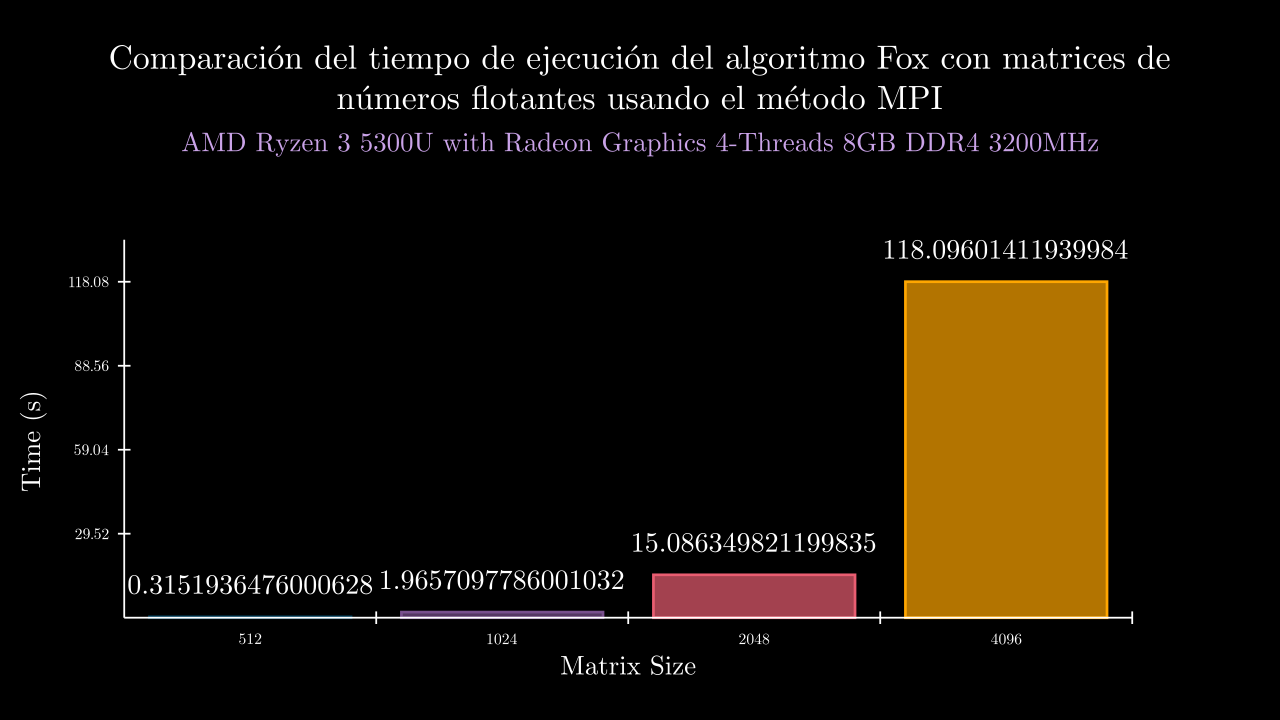
Float MPI Memory
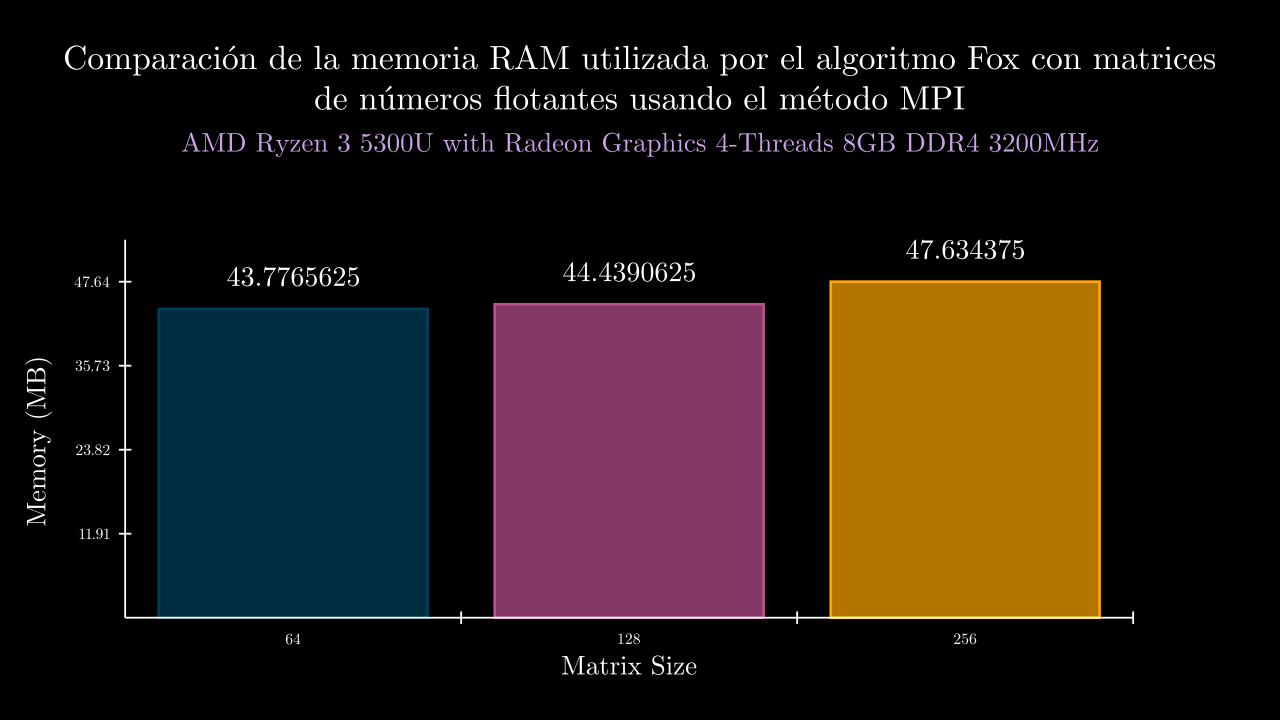
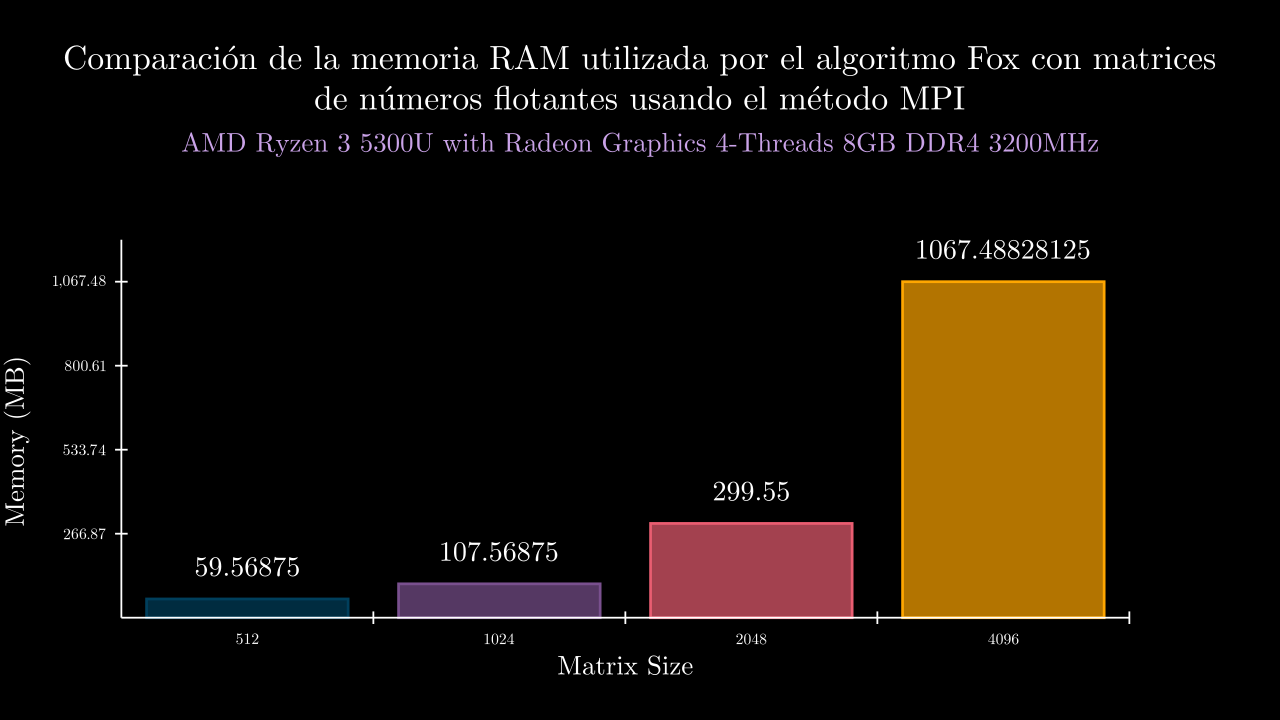
| exponent | time_mean | memory_mean | t1 | t2 | t3 | t4 | t5 | m1 | m2 | m3 | m4 | m5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 MPI | 0.006882413999846904 | 44827.2 | 0.00616076799997245 | 0.007571267999992415 | 0.009120849999817437 | 0.005788312999357004 | 0.005770871000095212 | 44516.0 | 44976.0 | 44856.0 | 44984.0 | 44804.0 |
| 7 MPI | 0.026216812000348 | 45505.6 | 0.0235308890005399 | 0.03057239500049036 | 0.030295870999907493 | 0.023232615000779333 | 0.023452290000022913 | 45340.0 | 45380.0 | 45916.0 | 45408.0 | 45484.0 |
| 8 MPI | 0.07103344159986591 | 48777.6 | 0.0644259669998064 | 0.07458897000014986 | 0.06409100400014722 | 0.08247323999967193 | 0.06958802699955413 | 48832.0 | 48752.0 | 48840.0 | 48740.0 | 48724.0 |
| 9 MPI | 0.31519364760006285 | 60998.4 | 0.3090453289996731 | 0.3105386739998721 | 0.323262332000013 | 0.328039964000709 | 0.305081939000047 | 60808.0 | 61292.0 | 61040.0 | 61132.0 | 60720.0 |
| 10 MPI | 1.9657097786001032 | 110150.4 | 1.956600716000139 | 1.972460088999469 | 1.967714929000067 | 1.963982125000257 | 1.9677910340005837 | 110216.0 | 110316.0 | 109880.0 | 110424.0 | 109916.0 |
| 11 MPI | 15.086349821199837 | 306739.2 | 15.097831608999513 | 15.06219048300045 | 15.081034732999797 | 15.11948033599947 | 15.071211944999959 | 306568.0 | 306676.0 | 306928.0 | 306700.0 | 306824.0 |
| 12 MPI | 118.09601411939984 | 1093108.0 | 117.49792914299996 | 117.55301655800031 | 117.4915157659998 | 120.29619238499981 | 117.64141674499933 | 1093068.0 | 1093104.0 | 1093056.0 | 1093292.0 | 1093020.0 |
| 6 SEC | 0.02014490380006464 | 134108.0 | 0.020155482000518532 | 0.02016766499946243 | 0.02030808099971182 | 0.0196520090003105 | 0.020441282000319916 | 134108.0 | 134108.0 | 134108.0 | 134108.0 | 134108.0 |
| 7 SEC | 0.050219269600347616 | 134108.0 | 0.04954443600036029 | 0.04997883800024283 | 0.051060316000075545 | 0.05030692000036652 | 0.05020583800069289 | 134108.0 | 134108.0 | 134108.0 | 134108.0 | 134108.0 |
| 8 SEC | 0.17468092960007198 | 134108.0 | 0.1734118699996543 | 0.17380072599917185 | 0.1739819490003356 | 0.17596849800065684 | 0.1762416050005413 | 134108.0 | 134108.0 | 134108.0 | 134108.0 | 134108.0 |
| 9 SEC | 0.8327643823999097 | 134108.0 | 0.8214600789997348 | 0.8339379310000368 | 0.8375314009999784 | 0.8423835240000699 | 0.8285089769997285 | 134108.0 | 134108.0 | 134108.0 | 134108.0 | 134108.0 |
| 10 SEC | 4.5236622611999335 | 134108.0 | 4.504509599000812 | 4.53639165200002 | 4.517755044999831 | 4.536735672999384 | 4.522919336999621 | 134108.0 | 134108.0 | 134108.0 | 134108.0 | 134108.0 |
| 11 SEC | 25.990362968200134 | 134108.0 | 26.099206627000058 | 26.0074372450008 | 26.028763903000254 | 25.8560191459992 | 25.960387920000358 | 134108.0 | 134108.0 | 134108.0 | 134108.0 | 134108.0 |
| 12 SEC | 168.52421300860004 | 426997.6 | 168.4287555890005 | 167.8469278450002 | 168.67190678299994 | 169.53767954900013 | 168.1357952769995 | 426988.0 | 426992.0 | 426944.0 | 426948.0 | 427116.0 |
Integer
Integer Sequential Time
Integer Sequential Memory
Integer MPI Time
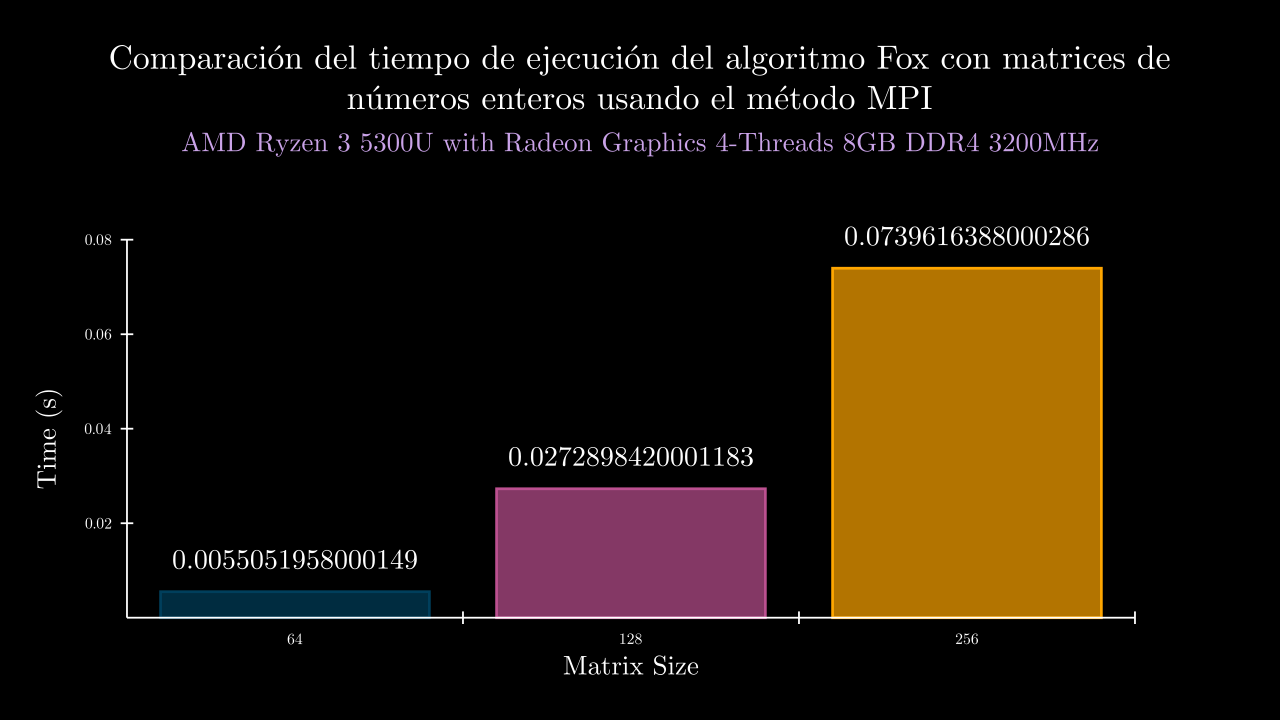
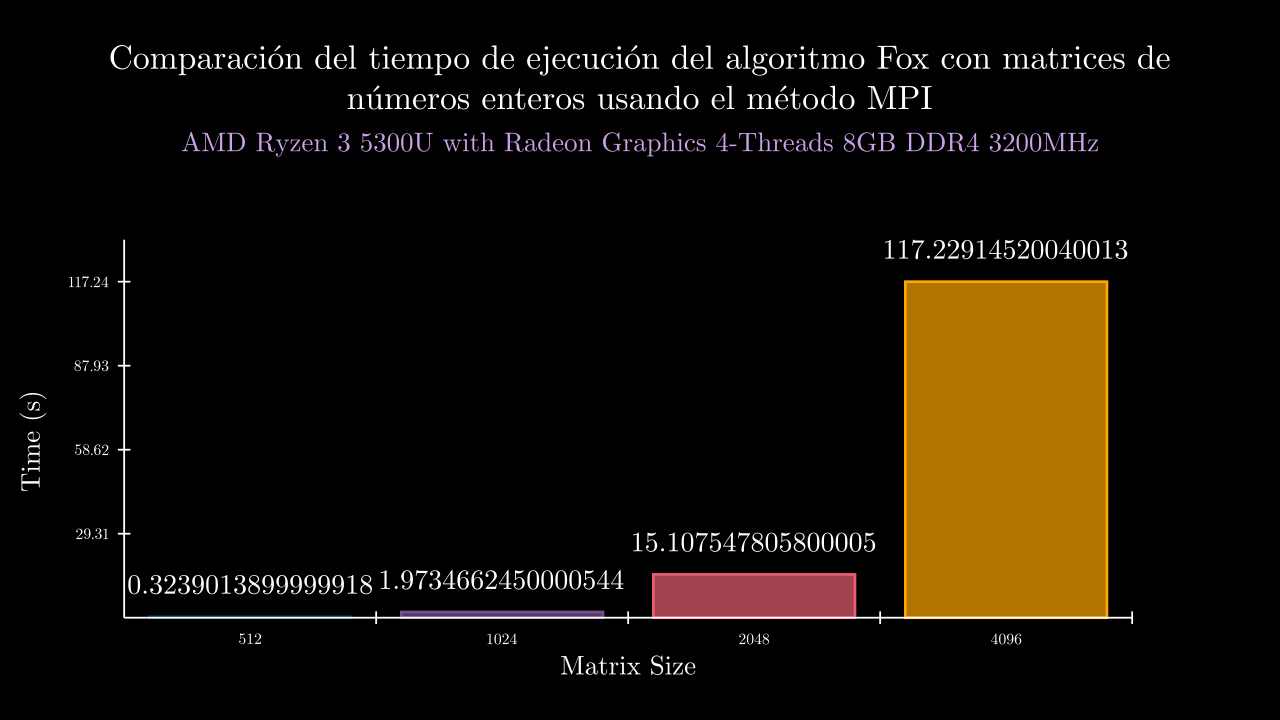
Integer MPI Memory
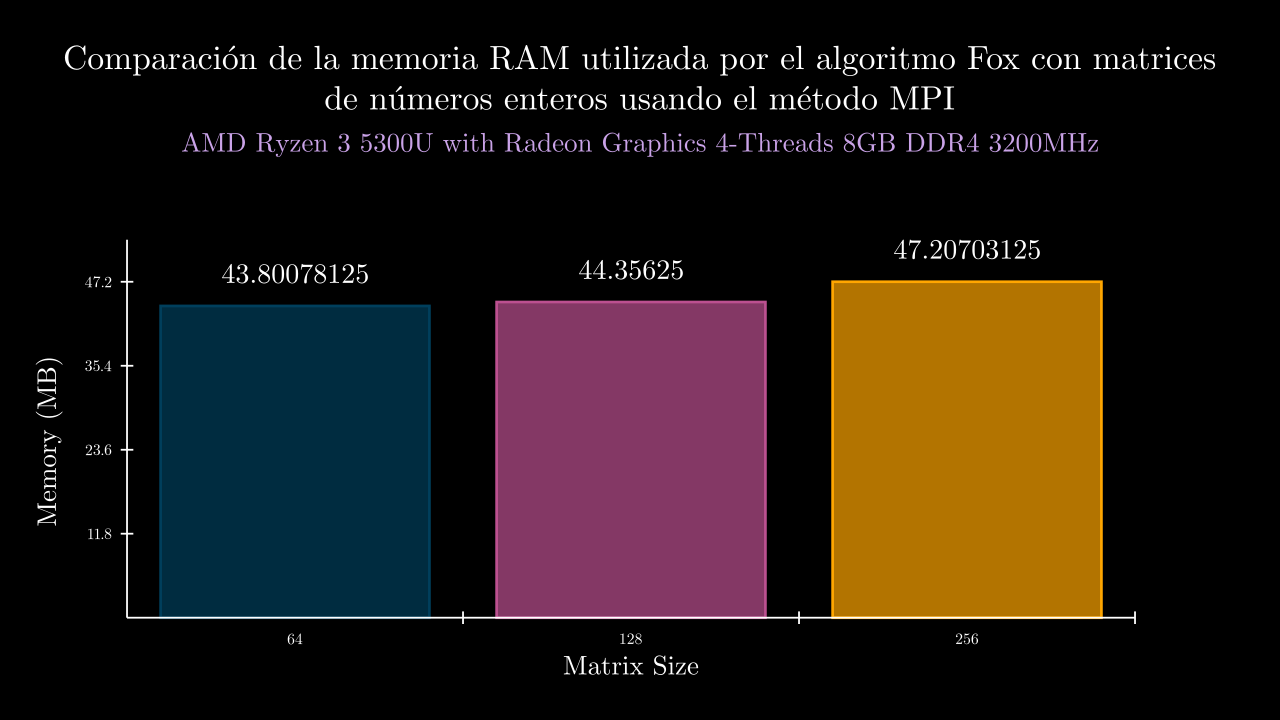
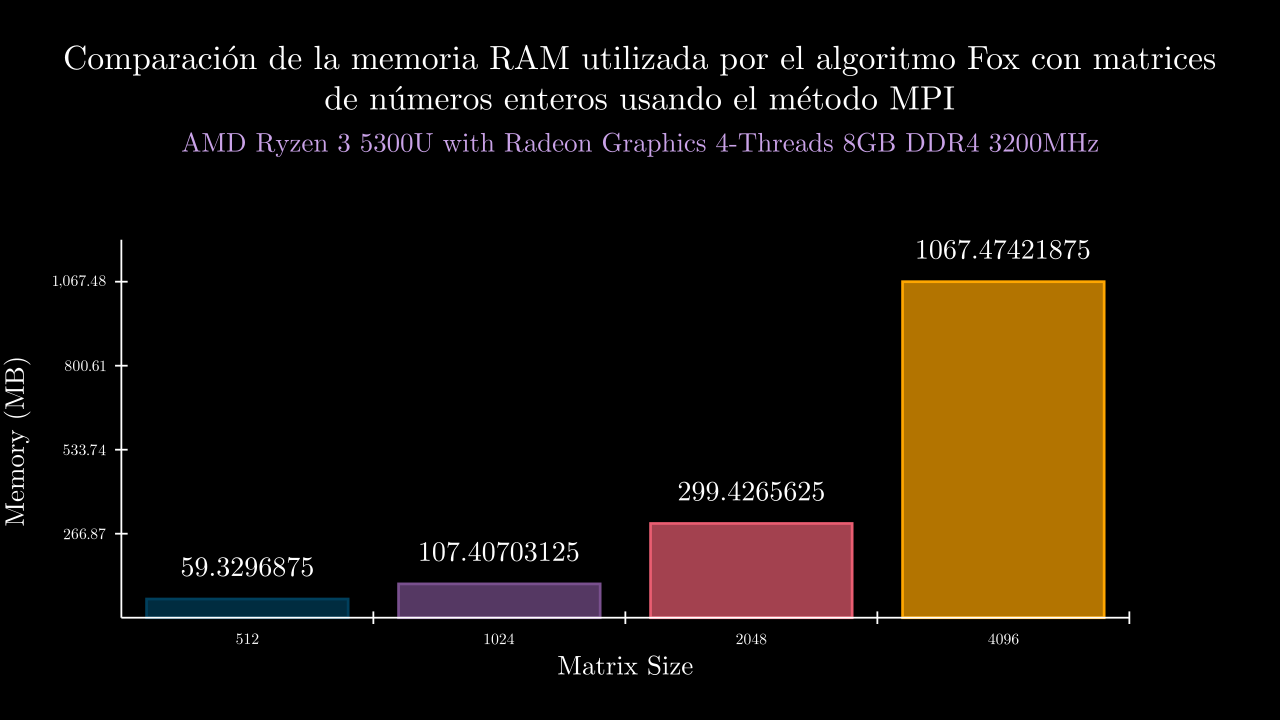
| exponent | time_mean | memory_mean | t1 | t2 | t3 | t4 | t5 | m1 | m2 | m3 | m4 | m5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 MPI | 0.0055051958000149 | 44852.0 | 0.0031517399997937 | 0.0057380630000807 | 0.0057468400000288 | 0.0040065170001071 | 0.008882819000064 | 44136.0 | 44744.0 | 45052.0 | 45140.0 | 45188.0 |
| 7 MPI | 0.0272898420001183 | 45420.8 | 0.0231502470001032 | 0.0234150100000078 | 0.0292151310000008 | 0.0348449370003436 | 0.0258238850001362 | 45544.0 | 44824.0 | 45760.0 | 45392.0 | 45584.0 |
| 8 MPI | 0.0739616388000286 | 48340.0 | 0.0729102610002883 | 0.0811236619997544 | 0.0858247690002826 | 0.0632901849999143 | 0.0666593169999032 | 48452.0 | 48448.0 | 47740.0 | 48440.0 | 48620.0 |
| 9 MPI | 0.3239013899999918 | 60753.6 | 0.3350273999999444 | 0.3262528649997875 | 0.3130012500000703 | 0.3336551950001194 | 0.3115702400000373 | 60692.0 | 60584.0 | 60768.0 | 60932.0 | 60792.0 |
| 10 MPI | 1.9734662450000544 | 109984.8 | 1.9745565680000248 | 1.973893446000148 | 1.9708118759999709 | 1.969781122999848 | 1.97828821200028 | 109884.0 | 110200.0 | 109584.0 | 110072.0 | 110184.0 |
| 11 MPI | 15.107547805800005 | 306612.8 | 15.11717991200021 | 15.073204916999655 | 15.11073724500011 | 15.112203008000051 | 15.124413946999994 | 306548.0 | 306824.0 | 306568.0 | 306516.0 | 306608.0 |
| 12 MPI | 117.22914520040013 | 1093093.6 | 117.3144714 | 117.3090739270001 | 117.34079946900056 | 117.31188550499974 | 116.86949570100025 | 1093016.0 | 1092912.0 | 1093332.0 | 1093060.0 | 1093148.0 |
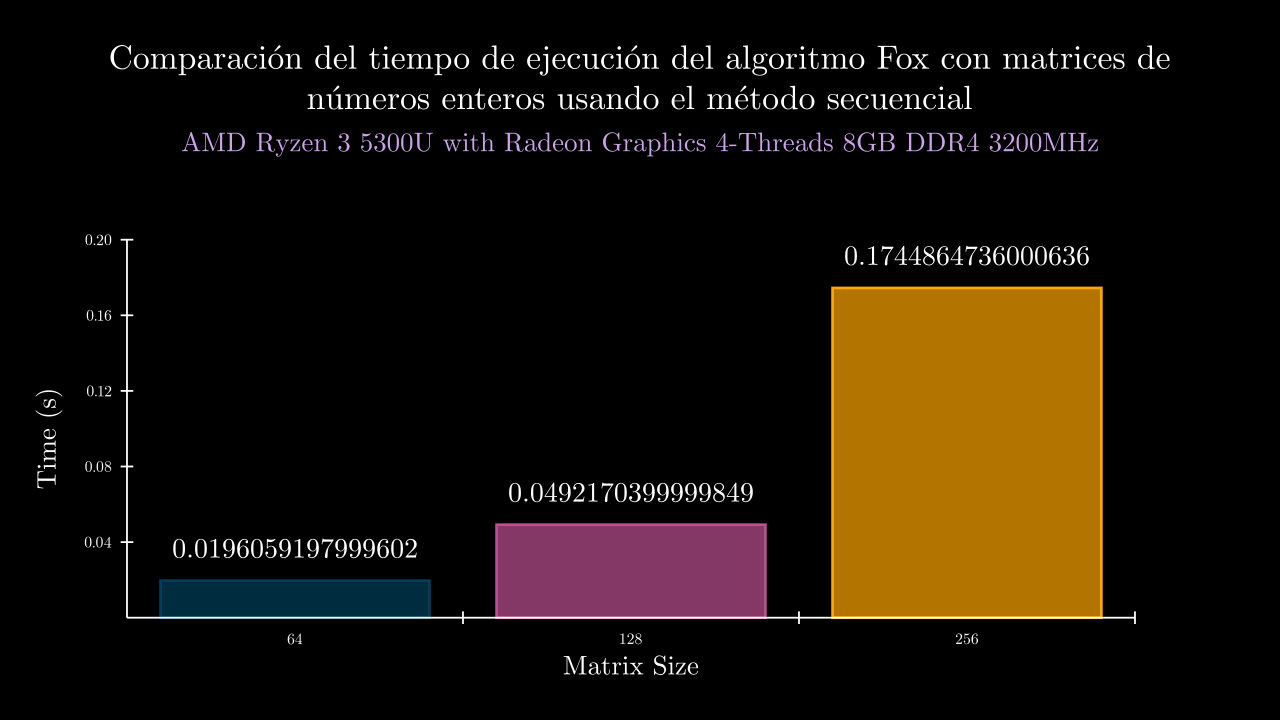
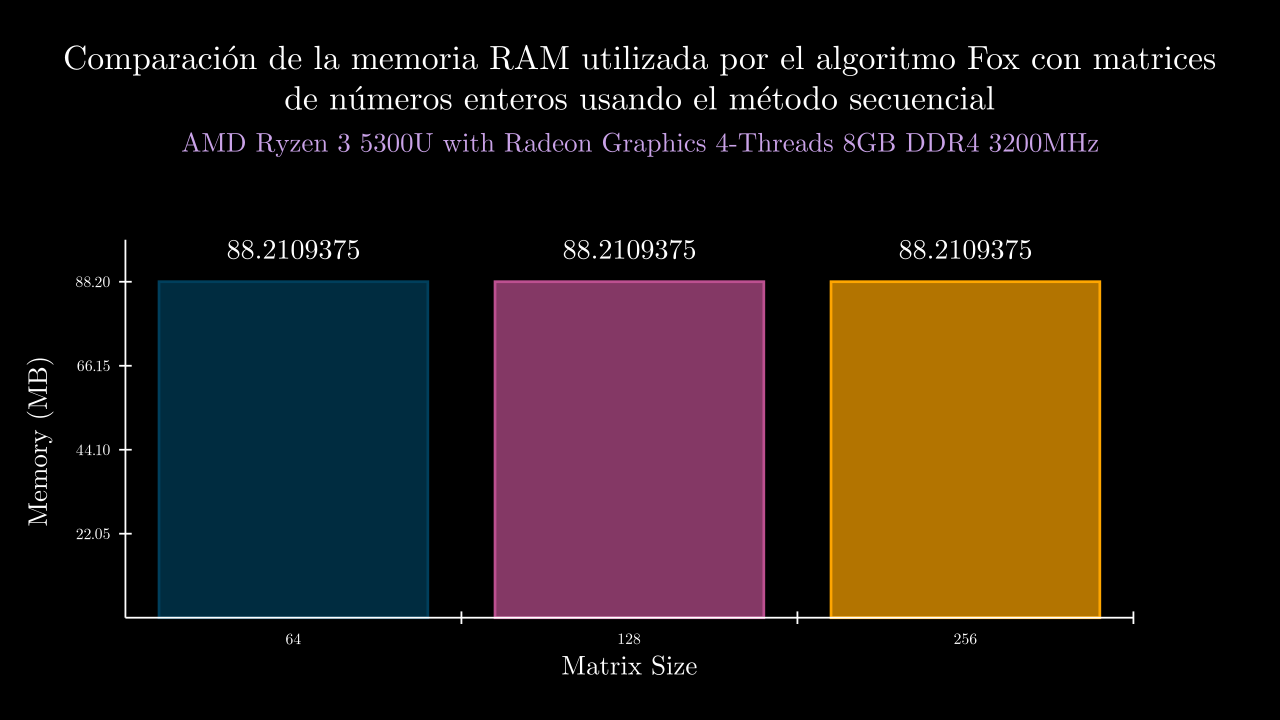
| 6 SEC | 0.0196059197999602 | 90328.0 | 0.0189724369997748 | 0.0196790810000493 | 0.020375796999815 | 0.0194069730000592 | 0.0195953110001028 | 90328.0 | 90328.0 | 90328.0 | 90328.0 | 90328.0 |
| 7 SEC | 0.0492170399999849 | 90328.0 | 0.0483742010001151 | 0.0493801659999917 | 0.0493045709999933 | 0.0496616390000781 | 0.0493646229997466 | 90328.0 | 90328.0 | 90328.0 | 90328.0 | 90328.0 |
| 8 SEC | 0.1744864736000636 | 90328.0 | 0.1772551020003447 | 0.1733394259999841 | 0.1735761519998959 | 0.1739198039999792 | 0.174341884000114 | 90328.0 | 90328.0 | 90328.0 | 90328.0 | 90328.0 |
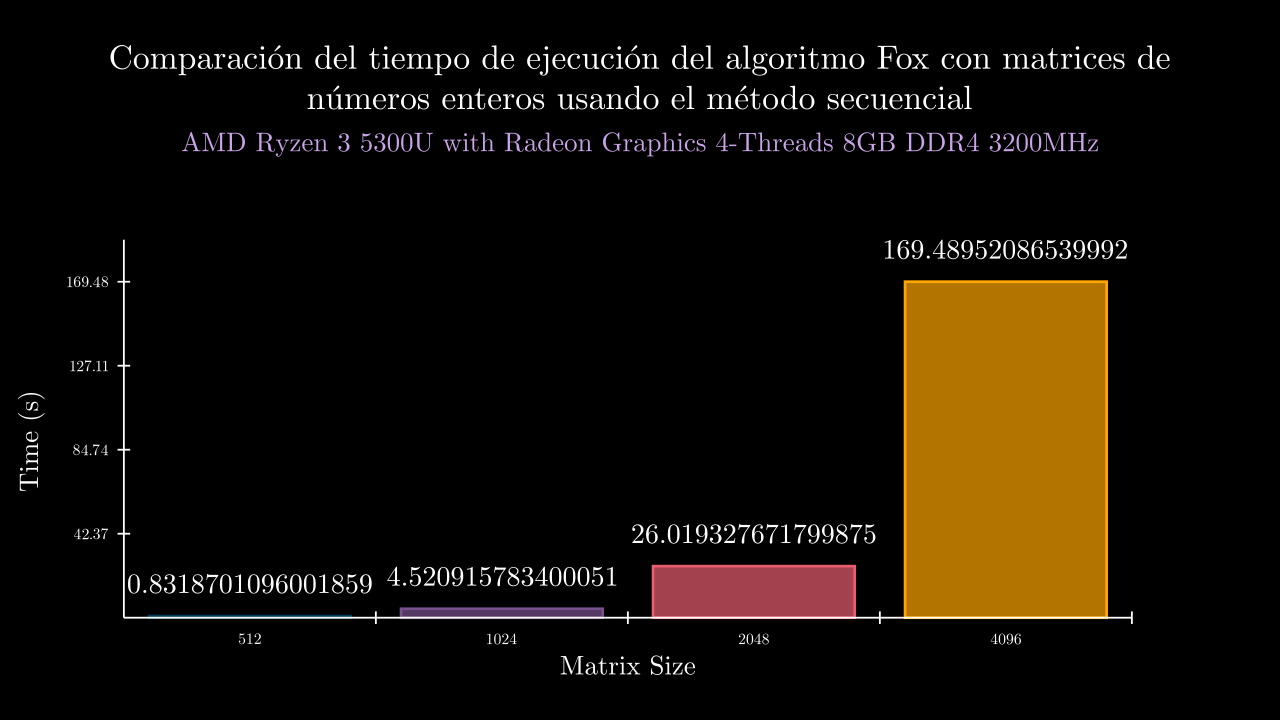
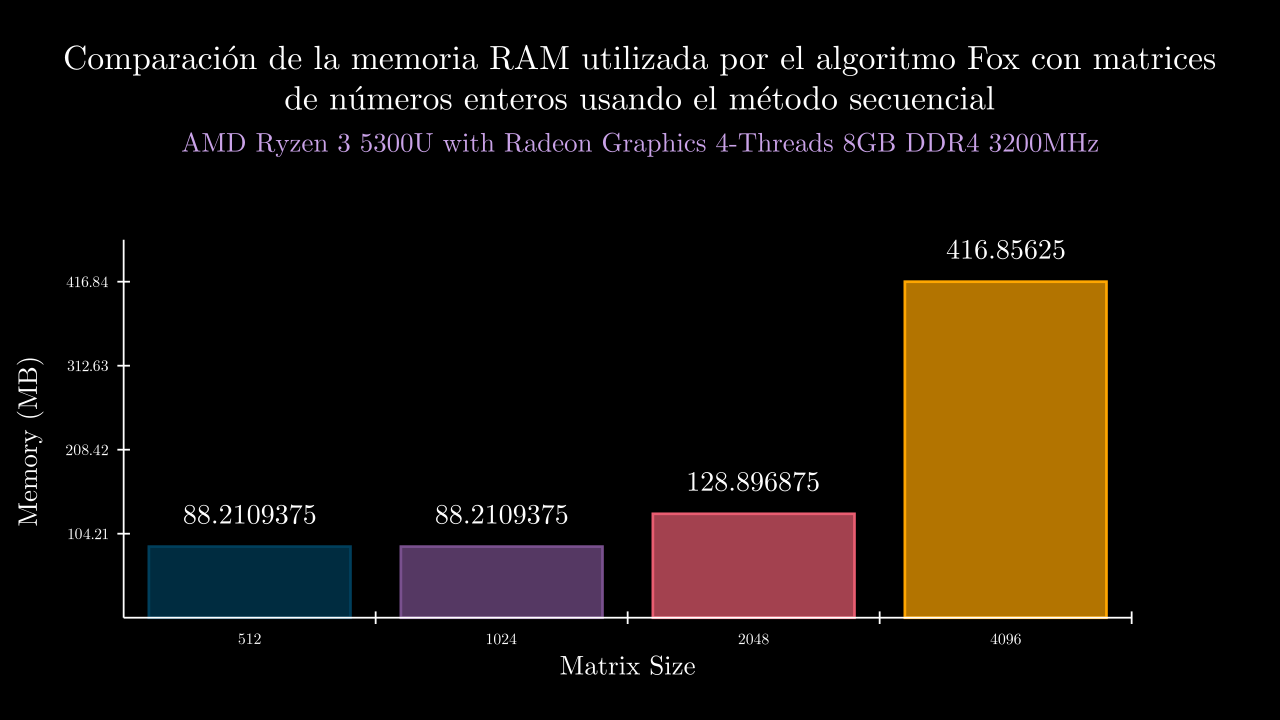
| 9 SEC | 0.8318701096001859 | 90328.0 | 0.8306139000001167 | 0.8401869850004005 | 0.8381296229999862 | 0.8236760620002315 | 0.8267439780001951 | 90328.0 | 90328.0 | 90328.0 | 90328.0 | 90328.0 |
| 10 SEC | 4.520915783400051 | 90328.0 | 4.518278625000221 | 4.515260805999787 | 4.517735109000114 | 4.488614104000135 | 4.5646902729999965 | 90328.0 | 90328.0 | 90328.0 | 90328.0 | 90328.0 |
| 11 SEC | 26.019327671799875 | 131990.4 | 25.927749363999737 | 25.88356371500004 | 25.887511626000105 | 26.452818032999858 | 25.944995620999634 | 131952.0 | 131952.0 | 131952.0 | 132144.0 | 131952.0 |
| 12 SEC | 169.48952086539992 | 426860.8 | 167.03305509500024 | 169.1147969169997 | 168.76519542999995 | 176.81053264399998 | 165.72402424099982 | 426904.0 | 426864.0 | 426868.0 | 426860.0 | 426808.0 |
Installation
This chapter explains how to test this implementation on both unix/linux and Windows based systems.
Linux Installation
For this installation we used:
- Arch Linux 2023.11.1 and Ubuntu 20.04 LTS
- Python 3.11.5
- pip 23.3.1
First, clone the github repository:
git clone https://github.com/miguehm/fox-algorithm.git && cd fox-algorithm
or alternatively, download the zip file and extract it:
Then, create a virtual environment
python3 -m venv venv
activate the virtual environment
source ./venv/bin/activate # for linux
and install requirements
pip install -r requirements.txt
Windows installation
For this installation we used:
- Windows 11 Nov 2023 update
- Python 3.11.5
- pip 23.3.1
You need to have MPI installed, you can download the installer from the microsoft official page.
First, clone the github repository:
git clone https://github.com/miguehm/fox-algorithm.git && cd fox-algorithm
or alternatively, download the zip file and extract it:

Then, create a virtual environment
python -m venv venv
activate the virtual environment
.\venv\Scripts\Activate
and install requirements
pip install -r requirements.txt
Usage
WARNING: The program will execute the algorithm for all the matrix sizes \(2^x\ \forall\ x \in [n, m]\). For values of \(n\) and \(m\) greater than 11, the execution time will be very long. For example, for \(n=11\) and \(m=12\), the execution time will be approximately 1 hour.
python3is for linux/unix OS based, if you have windows usepythoninstead.
Help
python3 src/main.py --help
Output
Usage: main.py [OPTIONS]
╭─ Options ─────────────────────────────────────╮
│ --help Show this message and exit. │
╰───────────────────────────────────────────────╯
╭─ Matrix order range ──────────────────────────╮
│ --min-exp INTEGER Exponent of base 2 │
│ matrix order (2^) │
│ [default: 6] │
│ --max-exp INTEGER Exponent of base 2 │
│ matrix order (2^) │
│ [default: 13] │
╰───────────────────────────────────────────────╯
╭─ MPI options ─────────────────────────────────╮
│ --threads INTEGER Number of cores to │
│ use │
│ [default: 4] │
╰───────────────────────────────────────────────╯
Default execution
python3 src/main.py
The execution will be done for the matrix of size \(2^6\) with 4 threads.
Multiple matrix multiplication by range
python3 src/main.py --min-exp 6 --max-exp 13
The charts with the results will be created in the charts folder.
Specify threads number
python3 src/main.py --threads 4
You can find out the number of threads available on your computer using
topcommand.